Question

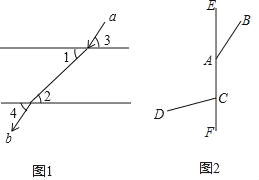
【题目】（1）光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学知识有∠1＝∠2，∠3＝∠4，请判断光线a与光线b是否平行，并说明理由；

（2）如图2，直线EF上有两点A、C，分别引两条射线AB、CD．已知∠BAF＝150°，∠DCF＝80°，射线AB、CD分别绕点A、点C以1度/秒和3度/秒的速度同时顺时针转动，设时间为t秒，当射线CD转动一周时，两条射线同时停止．则当直线CD与直线AB互相垂直时，t＝　 　秒．

Answer 1

【答案】（1）平行．理由见解析；（2）20或110．

【解析】

（1）依据题意得出∠1+∠5＝∠2+∠6，即可得到a∥b；

（2）分两种情况讨论：当BA⊥CD于G时，∠BAE＝30°+t°＝∠CAG，∠ACG＝180°﹣80°﹣3t°＝100°﹣3t°；当D'C⊥AB于H时，∠BAE＝30°+t°，∠ACH＝3t°﹣180°﹣100°，分别依据角的和差关系进行计算即可．

解：（1）平行．理由如下：

如图1，∵∠3＝∠4，

∴∠5＝∠6，

∵∠1＝∠2，

∴∠1+∠5＝∠2+∠6，

∴a∥b；

（2）如图，当BA⊥CD于G时，∠BAE＝30°+t°＝∠CAG，∠ACG＝180°﹣80°﹣3t°＝100°﹣3t°，

∵∠CAG+∠ACG＝90°，

∴30°+t°+100°﹣3t°＝90°，

解得t＝20；

如图，当D'C⊥AB于H时，∠BAE＝30°+t°，∠ACH＝3t°﹣180°﹣100°，

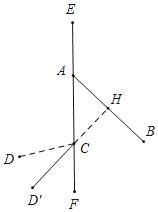
∵∠BAE＝∠ACH+∠AHC，

∴30°+t°＝3t°﹣180°﹣100°+90°，

解得t＝110，

综上所述，当直线CD与直线AB互相垂直时t的值为20或110．

故答案为：20或110．