【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣4a+4=0,则a= .b= .
(2)已知x2+2y2﹣2xy+6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长
参考答案:
【答案】(1)a=2,b=0;(2)xy=![]() ;(3)△ABC的周长为7
;(3)△ABC的周长为7
【解析】分析:(1)利用配方法将三项配方成完全平方式的形式,利用非负数的性质求得a、b的值即可;(2)利用配方法把原式变形,根据非负数的性质解答即可;(3)利用配方法把原式变形,根据非负数的性质和三角形三边关系解答即可;
本题解析:∵a![]() +b
+b![]() 4a+4=0,∴a
4a+4=0,∴a![]() 4a+4+b
4a+4+b![]() =0,∴(a2)
=0,∴(a2) ![]() +b
+b![]() =0,∴a2=0,b=0,
=0,∴a2=0,b=0,
解得a=2,b=0;
(2)∵x2+2y2﹣2xy+6y+9=0,∴x2+y2﹣2xy+y2+6y+9=0
即:(x﹣y)2+(y+3)2=0则:x﹣y=0,y+3=0,
解得:x=y=﹣3,∴xy=![]() =﹣
=﹣![]() ;
;
(3)∵2a2+b2﹣4a﹣6b+11=0,∴2a2﹣4a++2+b2﹣6b+9=0,
∴2(a﹣1)2+(b﹣3)2=0,则a﹣1=0,b﹣3=0,解得,a=1,b=3,
由三角形三边关系可知,三角形三边分别为1、3、3,
∴△ABC的周长为1+3+3=7;
故答案为: (1)a=2,b=0;(2)xy=![]() ;(3)△ABC的周长为7
;(3)△ABC的周长为7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个选项中,不是y关于x的函数的是( )
A.|y|=x﹣1 B.y=
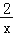 C.y=2x﹣7 D.y=x2
C.y=2x﹣7 D.y=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,BD=6,AD=3
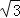 ,则∠AOD= 度.
,则∠AOD= 度.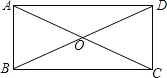
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:

①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A.①②③ B.①④⑤ C.①③④ D.③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=﹣x+b的图象与x轴、y轴分别交于点A、B,与函数y=2x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣x+b和y=2x的图象于点C,D.
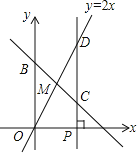
(1)求点A的坐标;
(2)若OB=CD,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示﹣0.00000123= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣b=3,ab=2,则a2+b2的值为 .
相关试题

