【题目】如图四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 的方向以每秒
的方向以每秒![]() 的速度运动到
的速度运动到![]() 点返回,动点
点返回,动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 停止运动,设运动时间为
停止运动,设运动时间为![]() (秒).
(秒).
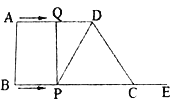

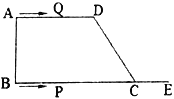

(1)当![]() 时,是否存在点
时,是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形,若存在,求出
是平行四边形,若存在,求出![]() 值;若不存在,请说明理由;
值;若不存在,请说明理由;
(2)当![]() 为何值时,以
为何值时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形面积等于
为顶点的四边形面积等于![]() ;
;
(3)当![]() 时,是否存在点
时,是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,请直接写出所有满足要求的
是等腰三角形?若存在,请直接写出所有满足要求的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)t=3;(2)t=![]() ;(3)t=3或t=
;(3)t=3或t=![]() .
.
【解析】
(1)当DQ=CP时,四边形PQDC是平行四边形,根据CP=153t,DQ=122t建立方程求解即可;
(2)分两种情况讨论:①当点P是从点B向点C运动时,②当点P从点C返回点B时,分别利用梯形面积公式构建方程,求出时间t,再舍去不合题意的值即可;
(3)分三种情况讨论:①当PQ=PD时,②当PQ=DQ时,③当DQ=PD时,分别利用等腰三角形的性质及勾股定理列方程解答即可.
解:(1)∵AD∥BC
∴当DQ=CP时,四边形PQDC是平行四边形,
当0<t<5时,点P从B运动到C,
∵DQ=ADAQ=122t,CP=153t,
∴122t=153t,
解得:t=3,
∴t=3时,四边形PQDC是平行四边形;
(2)分两种情况讨论:
①当点P是从点B向点C运动时,
∵CP=153t,DQ=122t,以C、D、Q、P为顶点的四边形面积等于30cm2,
∴S四边形CDQP=![]() (DQ+CP)AB=30,即
(DQ+CP)AB=30,即![]() × (122t+153t)×10=30,
× (122t+153t)×10=30,
解得:t=![]() ;
;
②当点P从点C返回点B时,
由运动知,DQ=122t,CP=3t15,
∴S四边形CDQP=![]() (DQ+CP)AB=30,即
(DQ+CP)AB=30,即![]() (122t+3t15)×10=30,
(122t+3t15)×10=30,
解得:t=9,
∵点Q到达点D的时间为12÷2=6,
∴t=9舍去,
∴当t为![]() 秒时,以C、D、Q、P为顶点的四边形面积等于30cm2;
秒时,以C、D、Q、P为顶点的四边形面积等于30cm2;
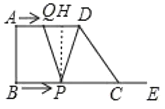
(3)分三种情况讨论:
作PH⊥AD于H,
①当PQ=PD时,则HQ=HD,
∵QH=HD=![]() DQ=
DQ=![]() (122t)=6t,
(122t)=6t,
由AH=BP,得:6t+2t=3t,
解得:t=3;
②当PQ=DQ时,
∵QH=AHAQ=BPAQ=3t2t=t,DQ=122t,
∴PQ2=QH2+PH2=t2+102,
∵DQ2=PQ2,
∴(122t)2=t2+102,
解得:t=![]() ,
,
∵0<t<5,
∴t=![]() ;
;
③当DQ=PD时,
∵DH=ADAH=ADBP=123t,DQ=122t,
∴PD2=PH2+HD2=102+(123t)2,
∵DQ2=PD2,
∴(122t)2=102+(123t)2,
整理得:5t224t+100=0,
∵△<0,
∴方程无实根,即此情况不存在,
综上可知,当t=3秒或t=![]() 秒时,△PQD是等腰三角形.
秒时,△PQD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光
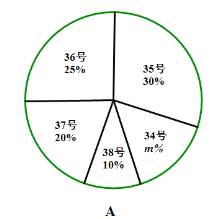
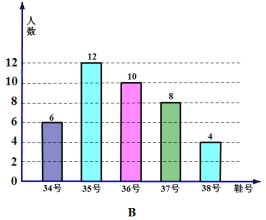
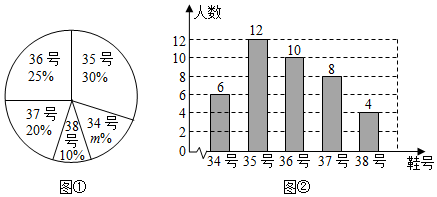 ,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:(1)本次随机抽样的学生数是多少?A中
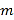 值是多少?
值是多少?(2)本次调查获取的样本数据的众数和中位数各是多少?
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的角平分线,点
的角平分线,点 ,
, 分别在
分别在 ,
, 上,且
上,且 ,
, .
.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)若
 ,
, ,求平行四边形
,求平行四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】银泰百货名创优品店购进600个钥匙扣,进价为每个8元,第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低
 元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,是用3根相同火柴棒拼成的一个三角图形,记为一个基本图形,将此基本图形不断的复制,使得相邻的两个基本图形的边重合,这样得到图②,图③…
(1)观察以上图形,图④中所用火柴棒的根数为_________,
猜想:在图n中,所用火柴棒的根数为_________(用n表示);
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(
 ,
, ),则
),则 =_________;
=_________;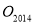 的坐标为_________.
的坐标为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则△DCE的面积为( )

A.
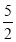 B.
B.  C. 2D. 1
C. 2D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市公共自行车服务公司调查某中学学生对公共自行车的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名学生,扇形统计图中
 .
.(2)请根据数据信息补全条形统计图,并求扇形统计图中“D类型”所对应的圆心角.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
相关试题

