【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
参考答案:
【答案】
(1)解:∵原方程有两个实数根,
∴△=(﹣2)2﹣4(m﹣1)≥0,
整理得:4﹣4m+4≥0,
解得:m≤2
(2)解:∵x1+x2=2,x1x2=m﹣1,x12+x22=6x1x2,
∴(x1+x2)2﹣2x1x2=6x1x2,
即4=8(m﹣1),
解得:m= ![]() .
.
∵m= ![]() <2,
<2,
∴符合条件的m的值为 ![]()
【解析】(1)根据一元二次方程x2﹣2x+m﹣1=0有两个实数根,可得△≥0,据此求出m的取值范围;(2)根据根与系数的关系求出x1+x2 , x1x2的值,代入x12+x22=6x1x2求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小颖在如图所示的四边形场地上,沿边骑自行车进行场地追逐赛(两人只要有一个人回到自己的出发点,则比赛结束).小明从A地出发,沿A→B→C→D→A的路线匀速骑行,速度为8米/秒;小颖从B地出发,沿B→C→D→A→B的路线匀速骑行,速度为6米/秒.已知∠ABC=90°,AB=40米,BC=80米,CD=90米.设骑行时间为t秒,假定他们同时出发且每转一个弯需要额外耗时2秒.
(1)填空:当t=_____秒时,两人第一次到B地的距离相等;
(2)试问小明能否在小颖到达D地前追上她?若能,求出此时t的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)x2+2x﹣9999=0
(2)2x2﹣2x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
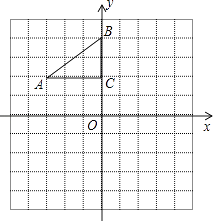
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
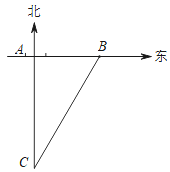
查看答案和解析>>【题目】如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为17cm,AB,CD是⊙O的两条弦,AB∥CD,AB=30cm,CD=16cm.求AB和CD之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB.
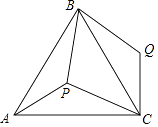
(1)求点P与点Q之间的距离;
(2)求∠APB的度数.
相关试题

