【题目】将直角三角板ABC绕直角顶点C逆时针旋转角度![]() ,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角
,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角![]() 的值为________.
的值为________.

参考答案:
【答案】20°或40°.
【解析】
先根据旋转的性质得∠BCE=α,CB=CE,再利用三角形内角和得到∠CBE=∠CEB=90°-![]() α,则∠EBF=∠CBE-∠CBA=60°-
α,则∠EBF=∠CBE-∠CBA=60°-![]() α,接着利用三角形外角性质得∠BFE=30°+α,然后分类讨论:当∠BFE=∠BEF时,即30°+α=60°-
α,接着利用三角形外角性质得∠BFE=30°+α,然后分类讨论:当∠BFE=∠BEF时,即30°+α=60°-![]() α或当∠BFE=∠BEF时,即30°+α=90°-
α或当∠BFE=∠BEF时,即30°+α=90°-![]() α,再分别解方程求出α即可.
α,再分别解方程求出α即可.
解:∵直角三角板ABC绕直角顶点C逆时针旋转角度α,得到△DCE,
∴∠BCE=α,CB=CE,
∴∠CBE=∠CEB=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,
α,
∴∠EBF=∠CBE-∠CBA=90°-![]() α-30°=60°-
α-30°=60°-![]() α,
α,
∵∠BFE=∠FCB+∠FBC,
∴∠BFE=30°+α,
又∵△BEF为等腰三角形,
∴当∠BFE=∠BEF时,即30°+α=60°-![]() α,解得α=20°;
α,解得α=20°;
当∠BFE=∠BEF时,即30°+α=90°-![]() α,解得α=40°,
α,解得α=40°,
即旋转角α的值为20°或40°.
故答案为20°或40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点P是BC边上一动点(不与点B、C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:

①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成。为了种植“花海”,需要从甲乙两地向大圩A.B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A.B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).
运费(元/吨)
A
B
甲地
12
12
乙地
10
8
(1)设甲地运往
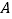 棚营养土
棚营养土 吨,请用关于
吨,请用关于 的代数式完成下表;
的代数式完成下表;运往A.B两地的吨数
A
B
甲地

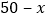
乙地
___
___
(2)设甲地运往A棚营养土
 吨,求总运费
吨,求总运费 (元)关于
(元)关于 (吨)的函数关系式(要求写出自变量取值范围).
(吨)的函数关系式(要求写出自变量取值范围).(3)当甲、乙两地各运往A.B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
-
科目: 来源: 题型:
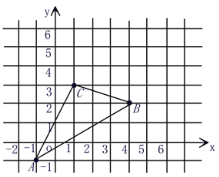
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)把△ABC向上平移3个单位,再向右平移2个单位得△A′B′C′,在图中画出两次平移后得到的图形△A′B′C′,并写出A′、B′、C′的坐标.
(2)如果△ABC内部有一点Q,根据(1)中所述平移方式得到对应点Q′,如果点Q′坐标是(m,n),那么点Q的坐标是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解该校七年级学生的身高情况,抽样调查了部分同学身高,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):
(1)请根据所提供的信息补全频数分布直方图;
(2)样本的中位数落在 (身高值)段中;
(3)如果该校七年级共有500名学生,那么估计全校身高在160cm或160cm以上的七年级学生有 人;
(4)如果上述七年级样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么 学生的身高比较整齐.(填“七年级”或“八年级”)

-
科目: 来源: 题型:
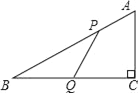
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
相关试题

