【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴、
轴、 ![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 ![]() 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
参考答案:
【答案】
(1)解:根据题意得![]() ,解得
,解得 ![]()
∴抛物线解析式为y=-x2+2x+3;
(2)解:当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3,则E(3,0);
y=-(x-1)2+4,则D(1,4),
∴S△ODE= ![]() ×3×4=6;
×3×4=6;
连接BE交直线x=1于点P,如图,则PA=PE, ∴PA+PB=PE+PB=BE, 此时PA+PB的值最小, 易得直线BE的解析式为 y=-x+3., 当x=1时,y=-x+3=3, ∴P(1,2).
【解析】(1)利用待定系数法将点A、B的坐标代入函数解析式,建立方程组,求解即可求出结果。
(2)先由y=0,解方程求出抛物线与x轴的交点E的坐标,,再求出抛物线的顶点坐标,利用三角形的面积公式求出△ODE的面积;连接BE交直线x=1于点P,利用两点之间线段最短,然后求出直线BE的解析式,易求出点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据绍兴市某风景区的旅游信息:
旅游人数
收费标准
不超过30人
人均收费80元
超过30人
每增加1人,人均收费降低1元,但人均收费不低于55元
A公司组织一批员工到该风景区旅游,支付给旅行社2800元.A公司参加这次旅游的员工有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数
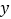 (件)与价格
(件)与价格  (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于
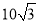 cm2?
cm2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B.
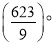 C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
36
52
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?
相关试题

