【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
参考答案:
【答案】C
【解析】分析:根据AD=AB和三角形内角和、外角性质,寻找∠C和∠BAC的关系的表达式;再根据BE=BC,寻找∠C和∠BAC关系的另一种表达式,由此可得关于∠BAC的方程,求得的度数,代入即可求得∠C.
详解:
∵AD=AB,
∴∠ADB=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC,
∠BAC,
∴∠C=∠ADB﹣∠DAC=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC﹣
∠BAC﹣![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() ∠BAC;
∠BAC;
∵BE=BC,
∴∠C=∠BEC=∠BAC+∠ABE=∠BAC+![]() (180°﹣
(180°﹣![]() ∠BAC)=∠BAC+45°﹣
∠BAC)=∠BAC+45°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
∴90°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
解得∠BAC=![]() ,
,
∴∠C=90°﹣![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=
 S四边形ABCD;⑤BC=CE.( )
S四边形ABCD;⑤BC=CE.( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数 1,3,5,7,9,…,排成如图的数阵.
(1)十字框中的五个数的和与中间数 15 有什么关系?
(2)设中间数为 a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于 2 005 吗?若能,请写出这五个数;若不能, 说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(﹣2,0),直线y=﹣
 x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点.
x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点. 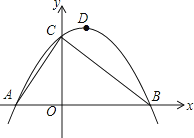
(1)请直接写出B、C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,但是由于
的小数部分我们不可能全部地写出来,但是由于 ,所以
,所以 的整数部分为1,将
的整数部分为1,将 减去其整数部分1,所得的差就是其小数部分
减去其整数部分1,所得的差就是其小数部分 ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题: 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______; 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______; 整数部分是______,小数部分是______;
整数部分是______,小数部分是______; 若设
若设 整数部分是x,小数部分是y,求
整数部分是x,小数部分是y,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
相关试题

