【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
参考答案:
【答案】(1)∠BCF=30°;(2)DE∥AB,见解析.
【解析】
(1)根据平行线的性质和已知求出∠2=∠1=∠B,即可得出答案;
(2)求出∠1=∠B=60°,根据平行线的性质求出∠ADC,求出∠ADE,即可得出∠1=∠ADE,根据平行线的判定得出即可.
(1)∵AD∥BC,
∴∠1=∠B=60°,
又∵∠1=∠2,
∴∠2=60°,
又∵FC⊥CD,
∴∠BCF=90°﹣60°=30°;
(2)DE∥AB.
证明:∵AD∥BC,∠2=60°,
∴∠ADC=120°,
又∵DE是∠ADC的平分线,
∴∠ADE=60°,
又∵∠1=60°,
∴∠1=∠ADE,
∴DE∥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数
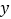 (件)与价格
(件)与价格  (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于
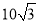 cm2?
cm2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与
与  轴、
轴、  轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B.
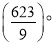 C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
36
52
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=2,则EC的长度为( )
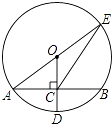
A.2
B.8
C.2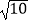
D.2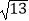
相关试题

