【题目】求代数式 ![]() 的最小值.
的最小值.
参考答案:
【答案】解:求代数式 ![]() 的最小值.可以转化为在x轴上求一点P(x,0),使得点P到点A(0,2),点B(12,3)的距离之和最小. 如图,作点A关于x轴的对称点A′,连接BA′由x轴的交点即为点P,作BM⊥y轴于M,
的最小值.可以转化为在x轴上求一点P(x,0),使得点P到点A(0,2),点B(12,3)的距离之和最小. 如图,作点A关于x轴的对称点A′,连接BA′由x轴的交点即为点P,作BM⊥y轴于M,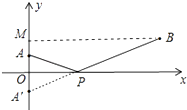
因为PA+PB的最小值=BA′= ![]() =
= ![]() =13.
=13.
所以代数式 ![]() 的最小值为13
的最小值为13
【解析】求代数式 ![]() 的最小值.可以转化为在x轴上求一点P(x,0),使得点P到点A(0,2),点B(12,3)的距离之和最小.如图,作点A关于x轴的对称点A′,连接BA′由x轴的交点即为点P,作BM⊥y轴于M,利用勾股定理即可解决问题.
的最小值.可以转化为在x轴上求一点P(x,0),使得点P到点A(0,2),点B(12,3)的距离之和最小.如图,作点A关于x轴的对称点A′,连接BA′由x轴的交点即为点P,作BM⊥y轴于M,利用勾股定理即可解决问题.
【考点精析】通过灵活运用轴对称-最短路线问题,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径即可以解答此题.
-
科目: 来源: 题型:
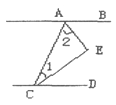
查看答案和解析>>【题目】如图,已知AB∥CD,CE、AE分别平分
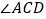 、
、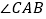 ,则
,则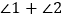 = ( )
= ( )
A.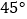
B.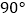
C.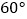
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用分解因式计算:
(1)2022+202×196+982
(2)(﹣2)100+(﹣2)100.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a15÷b5=a3B. 4a3a2=12a2
C. (a﹣b)2=a2﹣b2D. (2a2)2=4a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能镶嵌成平面图案的正多边形组合为( )
A.正八边形和正方形
B.正五边形和正十边形
C.正六边形和正三角形
D.正六边形和正八边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
 x2﹣(m﹣3)x+m2=0有两个不相等的实数根,那么m的最大整数值是( )
x2﹣(m﹣3)x+m2=0有两个不相等的实数根,那么m的最大整数值是( )
A.2
B.1
C.0
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】模拟x2﹣6x=1,左边配成一个完全平方式得( )
A.(x﹣3)2=10
B.(x﹣3)2=9
C.(x﹣6)2=8
D.(x﹣6)2=10
相关试题

