搜索
【题目】已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．
（1）画出△ABC向上平移6个单位得到的△A1B1C1；
（2）以点C为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标．
参考答案：
【答案】（1）作图见解析；（2）作图见解析；A2坐标（﹣2，﹣2）．
【解析】试题分析(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用位似图形的性质得出对应点的位置进而得出.
试题解析:⑴如图所示: △A1B1C1,即为所求；⑵如图所示△A2B2C2，即为所求；A2坐标(－2，－2)
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表：
(1)若工厂计划获利14万元，问A、B两种产品应分别生产多少件？
(2)若工厂投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？
(3)在(2)条件下，哪种方案获利最大？并求最大利润．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，已知点A（0，a），B（0，b）在y轴上，点 C（m，b）是第四象限内一点，且满足
，△ABC的面积是56；AC交x轴于点D，E是y轴负半轴上的一个动点.(1)求C点坐标；
(2)如图2，连接DE，若DE
AC于D点，EF为∠AED的平分线，交x轴于H点，且∠DFE＝90°，求证：FD平分∠ADO；(3)如图3，E在y轴负半轴上运动时，连EC，点P为AC延长线上一点，EM平分 ∠AEC，且PM⊥EM于M点，PN⊥x轴于N点，PQ平分∠APN，交x轴于Q点，则E在运动过程中，
的大小是否发生变化，若不变，求出其值；若变化，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：① BC平分∠ABE；② AC∥BE；③ ∠CBE+∠D＝90°；④ ∠DEB＝2∠ABC．其中正确结论的个数有（ ）
A.1个B.2个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于x的一次函数y=(2m-1)x+m -2，若它的函数值y随x的增大而增大，且图象与y轴负半轴相交，且m为正整数．
（1）求这个函数的解析式．
（2）求直线y=－x和（1）中函数的图象与x轴围成的三角形面积．
-
科目： 来源： 题型：
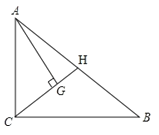
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，点G是△ABC的重心，且AG⊥CG，CG的延长线交AB于H．
（1）求证：△CAG∽△ABC；
（2）求S△AGH：S△ABC的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
的图象与x轴交于A、B两点，与y轴交于C点，已知点B坐标为（4，0）．
（1）求抛物线的解析式；
（2）判断△ABC的形状，直接写出△ABC外接圆的圆心坐标．
相关试题
