【题目】直线AB∥CD,点P在两平行线之间,点E. F分别在AB、CD上,连接PE,PF.尝试探究并解答:
(1)若图1中∠1=36°,∠2=63°,则∠3=___;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2所示,∠1与∠3的平分线交于点P`,若∠2=α,试求∠EP`F的度数(用含α的代数式表示);
(4)如图3所示,在图2的基础上,若∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,∠BEP
,∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() …∠BEP
…∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,且∠2=α,直接写出∠EP
,且∠2=α,直接写出∠EP![]() F的度数(用含α的代数式表示).
F的度数(用含α的代数式表示).
参考答案:
【答案】(1)27°;(2)∠2=∠1+∠3;(3)![]() α;(4)
α;(4)![]() α;
α;
【解析】
(1)利用结论:∠2=∠1+∠3计算即可.
(2)结论:∠2=∠1+∠3.如图1中,作PM∥AB.利用平行线的性质证明即可.
(3)利用(2)中结论以及角平分线的定义即可解决问题.
(4)探究规律,利用规律解决问题即可.
(1)∠3=∠2∠1=63°36°=27°.
故答案为27°.
(2)结论:∠2=∠1+∠3.
理由:如图1中,作PM∥AB.
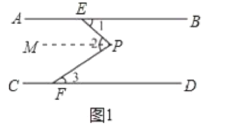
∵AB∥CD,AB∥PM,
∴PM∥CD,
∴∠1=∠MPE,∠3=∠MPF,
∴∠2=∠1+∠3.
(3)如图2中,
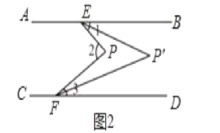
∵∠BEP+∠DFP=∠2=α,
∴∠EP′F=∠BEP′+∠DFP′=![]() (∠BEP+∠DFP)=
(∠BEP+∠DFP)=![]() α.
α.
(4)如图3中,
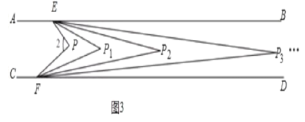
由(3)可知:∠P![]() =
=![]() α,∠P
α,∠P![]() =(
=(![]() )
)![]() α,∠P
α,∠P![]() =(
=(![]() )
)![]() α,…,∠P
α,…,∠P![]() =
=![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 ,
, 与
与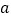 ,
, 分别相交于点
分别相交于点 ,
, ,且
,且 ,
, 交直线
交直线 于点
于点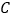 .
.
(1)若
 ,求
,求 的度数;
的度数;(2)若
 ,
,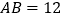 ,
, ,求直线
,求直线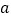 与
与 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对
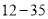 岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.请根据图中的信息,解决下列问题:
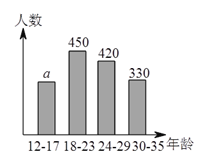
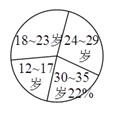
(
 )求条形统计图中
)求条形统计图中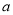 的值.
的值.(
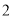 )求扇形统计图中
)求扇形统计图中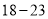 岁部分所占的百分比;
岁部分所占的百分比;(
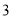 )据报道,目前我国
)据报道,目前我国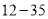 岁网瘾人数约为
岁网瘾人数约为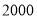 万,请估计其中
万,请估计其中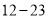 岁的人数.
岁的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到
 (点
(点 与点D对应).若OD=3,求点
与点D对应).若OD=3,求点 的坐标.
的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )

A.(S.S.S.) B.(S.A.S.) C.(A.S.A.) D.(A.A.S.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
 (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)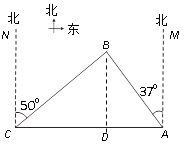
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将1、
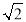 、
、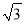 三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(9,3)与(2019,2019)表示的两个数的积是( )
三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(9,3)与(2019,2019)表示的两个数的积是( )
A.1B.2C.3D.
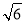
相关试题

