【题目】网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对![]() 岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
请根据图中的信息,解决下列问题:
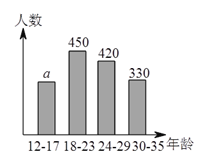
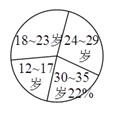
(![]() )求条形统计图中
)求条形统计图中![]() 的值.
的值.
(![]() )求扇形统计图中
)求扇形统计图中![]() 岁部分所占的百分比;
岁部分所占的百分比;
(![]() )据报道,目前我国
)据报道,目前我国![]() 岁网瘾人数约为
岁网瘾人数约为![]() 万,请估计其中
万,请估计其中![]() 岁的人数.
岁的人数.
参考答案:
【答案】(![]() )3000;(
)3000;(![]() )
)![]() ;(
;(![]() )
)![]() 万人.
万人.
【解析】分析:(1)用30~35岁的人数除以所占的百分比求出被调查的人数,然后列式计算即可得解;(2)用360°乘以18~23岁的人数所占的百分比计算即可得解;(3)用网瘾总人数乘以12~35岁的人数所占的百分比计算即可得解.
本题解析:
(![]() )被调查人数
)被调查人数![]() (人),
(人),
∴![]() (人).
(人).
(![]() )
)![]() 岁部分所占百分比为
岁部分所占百分比为![]() .
.
(![]() )∵
)∵![]() 岁网瘾人数均为
岁网瘾人数均为![]() 万,
万,
∴![]() 岁人数约为
岁人数约为![]() 万
万![]() 万.
万.
答:其中![]() 为
为![]() 万人.
万人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有.注:古代一斗是10升.

大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.
(1)列方程求壶中原有多少升酒;
(2)设壶中原有
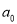 升酒,在第n个店饮酒后壶中余
升酒,在第n个店饮酒后壶中余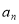 升酒,如第一次饮后所余酒为
升酒,如第一次饮后所余酒为 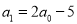 (升),第二次饮后所余酒为
(升),第二次饮后所余酒为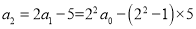 (升),……
(升),…… ① 用含
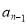 的式子表示
的式子表示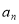 = ,再用含
= ,再用含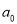 和n的式子表示
和n的式子表示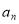 = ;
= ; ② 按照这个约定,如果在第4个店喝光了壶中酒,请借助①中的结论求壶中原有多少升酒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过一个多边形的某一顶点共可作2017条对角线,则这个多边形的边数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说明中正确的是( )
A.同位角相等
B.如果一个等腰三角形的两边长分别为3和6,那么该三角形的周长为12或15
C.直线外一点与直线上各点连接的所有线段中,垂线段最短
D.事件“打开电视机,正好播放足球比赛”是必然事件 -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣2,a)和点B(b,﹣5)关于x轴对称,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣3x2+12x﹣7的顶点坐标为( )
A.(2,5)
B.(2,﹣19)
C.(﹣2,5)
D.(﹣2,﹣43) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a+3b=5ab B.a2·a4=a8 C.(-2a2b)3=-8a6b3 D.a6÷a3+a2=2a2
相关试题

