【题目】有这样一个问题:探究函数y= ![]() 的图象与性质. 下面是小文的探究过程,请补充完整:
的图象与性质. 下面是小文的探究过程,请补充完整:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | 0 | 2 | | | | … |
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点A1和B1 , A2和B2 , A3和B3 , A4和B4均关于某点中心对称,则该点的坐标为;
②小文分析函数y= ![]() 的表达式发现:当x<1时,该函数的最大值为0,则该函数图象在直线x=1左侧的最高点的坐标为;
的表达式发现:当x<1时,该函数的最大值为0,则该函数图象在直线x=1左侧的最高点的坐标为;
(3)小文补充了该函数图象上两个点( ![]() ,﹣
,﹣ ![]() ),(
),( ![]() ,
, ![]() ), ①在上图中描出这两个点,并画出该函数的图象;
), ①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质: .
参考答案:
【答案】
(1)x≠1
(2)(1,1);(0,0)
(3) ;当x>1时,该函数的最小值为1
;当x>1时,该函数的最小值为1
【解析】解:(1)依题意得:2x﹣2≠0,解得x≠1,故答案是:x≠1;(2)①点A1和B1 , A2和B2 , A3和B3 , A4和B4均关于某点中心对称,A1(0,0),B2(2,2),∴中心点点坐标为(1,1);②∵当x<1时,该函数的最大值为0, ∴该函数图象在直线x=1左侧的最高点的坐标为(0,0);所以答案是(1,1);(0,0);(3)②该函数的性质:(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.(ⅳ)当x>1时,该函数的最小值为1.所以答案是当x>1时,该函数的最小值为1.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
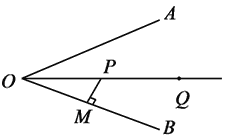
查看答案和解析>>【题目】已知:BOA是一条公路,河流OP恰好经过桥O平分∠AOB.
(1)如果要从P处移动到公路上路径最短,除图中所示PM外,还可以选择PN,求作这条路径,两条路径的关系是______,理由是___________.
(2)河流下游处有一点Q,如果要从P点出发,到达公路OA上的点C后再前往点Q,请你画出一条最短路径,表明点C的位置.
(3)D点在公路OB上,O点到D点的距离与C点相等,作出△CDP,求证:△CDP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用白铁皮做罐头盒,每张铁皮可做盒身25个,或做盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
①设用x张制盒身,可得方程2×25x=40(36﹣x);
②设用x张制盒身,可得方程25x=2×40(36﹣x);
③设用x张制盒身,y张制盒底,可得方程组
 ;
;④设用x张制盒身,y张制盒底,可得方程组
 ;其中正确的是( )
;其中正确的是( )A. ①④ B. ②③ C. ②④ D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,抛物线y=mx2﹣2m2x+2交y轴于A点,交直线x=4于B点.
(1)抛物线的对称轴为x=(用含m的代数式表示);
(2)若AB∥x轴,求抛物线的表达式;
(3)记抛物线在A,B之间的部分为图象G(包含A,B两点),若对于图象G上任意一点P(xp , yp),yp≤2,求m的取值范围.
相关试题

