【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.

参考答案:
【答案】(1)详见解析;(2)∠BDE=20°.
【解析】
(1)根据已知条件易证BC∥DF,根据平行线的性质可得∠F=∠PBC;再利用同角的补角相等证得∠F=∠PCB,所以∠PBC=∠PCB,由此即可得出结论;(2)连接OD,先证明四边形DHBC是平行四边形,根据平行四边形的性质可得BC=DH=1,在Rt△ABC中,用锐角三角函数求出∠ACB=60°,进而判断出DH=OD,求出∠ODH=20°,再求得∠NOH=∠DOC=40°,根据三角形外角的性质可得∠OAD=![]() ∠DOC=20°,最后根据圆周角定理及平行线的性质即可求解.
∠DOC=20°,最后根据圆周角定理及平行线的性质即可求解.
(1)如图1,∵AC是⊙O的直径,
∴∠ABC=90°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠DEA=∠ABC,
∴BC∥DF,
∴∠F=∠PBC,
∵四边形BCDF是圆内接四边形,
∴∠F+∠DCB=180°,
∵∠PCB+∠DCB=180°,
∴∠F=∠PCB,
∴∠PBC=∠PCB,
∴PC=PB;
(2)如图2,连接OD,
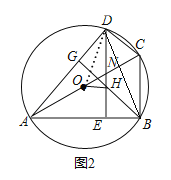
∵AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥DC,
∵BC∥DE,
∴四边形DHBC是平行四边形,
∴BC=DH=1,
在Rt△ABC中,AB=![]() ,tan∠ACB=
,tan∠ACB=![]() ,
,
∴∠ACB=60°,
∴BC=![]() AC=OD,
AC=OD,
∴DH=OD,
在等腰△DOH中,∠DOH=∠OHD=80°,
∴∠ODH=20°,
设DE交AC于N,
∵BC∥DE,
∴∠ONH=∠ACB=60°,
∴∠NOH=180°﹣(∠ONH+∠OHD)=40°,
∴∠DOC=∠DOH﹣∠NOH=40°,
∵OA=OD,
∴∠OAD=![]() ∠DOC=20°,
∠DOC=20°,
∴∠CBD=∠OAD=20°,
∵BC∥DE,
∴∠BDE=∠CBD=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c过点A(0,2).
(1)若点(﹣
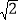 ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.
①求抛物线的解析式;
②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.

(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.

相关试题

