【题目】已知抛物线y=ax2+bx+c过点A(0,2).
(1)若点(﹣![]() ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;
(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.
①求抛物线的解析式;
②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.
参考答案:
【答案】(1)2a﹣![]() b+2=0(a≠0);(2)①y=﹣x2+2;②详见解析.
b+2=0(a≠0);(2)①y=﹣x2+2;②详见解析.
【解析】
(1)由抛物线经过点A可求出c=2,再把(﹣![]() ,0)代入抛物线的解析式,即可得2a﹣
,0)代入抛物线的解析式,即可得2a﹣![]() b+2=0(a≠0);
b+2=0(a≠0);
(2)①根据二次函数的性质可得出抛物线的对称轴为y轴、开口向下,进而可得出b=0,由抛物线的对称性可得出△ABC为等腰三角形,结合其有一个60°的内角可得出△ABC为等边三角形,设线段BC与y轴交于点D,根据等边三角形的性质可得出点C的坐标,再利用待定系数法可求出a值,即可求得抛物线的解析式;②由①的结论可得出点M的坐标为(x1,﹣![]() +2)、点N的坐标为(x2,﹣
+2)、点N的坐标为(x2,﹣![]() +2),由O、M、N三点共线可得出x2=﹣
+2),由O、M、N三点共线可得出x2=﹣![]() ,进而可得出点N及点N′的坐标,由点A、M的坐标利用待定系数法可求出直线AM的解析式,利用一次函数图象上点的坐标特征可得出点N′在直线PM上,进而即可证出PA平分∠MPN.
,进而可得出点N及点N′的坐标,由点A、M的坐标利用待定系数法可求出直线AM的解析式,利用一次函数图象上点的坐标特征可得出点N′在直线PM上,进而即可证出PA平分∠MPN.
(1)∵抛物线y=ax2+bx+c过点A(0,2),
∴c=2.
又∵点(﹣![]() ,0)也在该抛物线上,
,0)也在该抛物线上,
∴a(﹣![]() )2+b(﹣
)2+b(﹣![]() )+c=0,
)+c=0,
∴2a﹣![]() b+2=0(a≠0).
b+2=0(a≠0).
(2)①∵当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0,
∴x1﹣x2<0,y1﹣y2<0,
∴当x<0时,y随x的增大而增大;
同理:当x>0时,y随x的增大而减小,
∴抛物线的对称轴为y轴,开口向下,
∴b=0.
∵OA为半径的圆与拋物线的另两个交点为B、C,
∴△ABC为等腰三角形,
又∵△ABC有一个内角为60°,
∴△ABC为等边三角形.
设线段BC与y轴交于点D,则BD=CD,且∠OCD=30°,
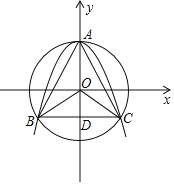
又∵OB=OC=OA=2,
∴CD=OCcos30°=![]() ,OD=OCsin30°=1.
,OD=OCsin30°=1.
不妨设点C在y轴右侧,则点C的坐标为(![]() ,﹣1).
,﹣1).
∵点C在抛物线上,且c=2,b=0,
∴3a+2=﹣1,
∴a=﹣1,
∴抛物线的解析式为y=﹣x2+2.
②证明:由①可知,点M的坐标为(x1,﹣![]() +2),点N的坐标为(x2,﹣
+2),点N的坐标为(x2,﹣![]() +2).
+2).
直线OM的解析式为y=k1x(k1≠0).
∵O、M、N三点共线,
∴x1≠0,x2≠0,且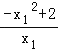 =
=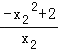 ,
,
∴﹣x1+![]() =﹣x2+
=﹣x2+![]() ,
,
∴x1﹣x2=﹣![]() ,
,
∴x1x2=﹣2,即x2=﹣![]() ,
,
∴点N的坐标为(﹣![]() ,﹣
,﹣![]() +2).
+2).
设点N关于y轴的对称点为点N′,则点N′的坐标为(![]() ,﹣
,﹣![]() +2).
+2).
∵点P是点O关于点A的对称点,
∴OP=2OA=4,
∴点P的坐标为(0,4).
设直线PM的解析式为y=k2x+4,
∵点M的坐标为(x,﹣![]() +2),
+2),
∴﹣![]() +2=k2x1+4,
+2=k2x1+4,
∴k2=﹣![]() ,
,
∴直线PM的解析式为y=﹣![]() +4.
+4.
∵﹣![]()
![]() +4=
+4=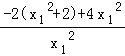 =﹣
=﹣![]() +2,
+2,
∴点N′在直线PM上,
∴PA平分∠MPN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=
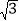 ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.

(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D( ),E( ),F( );
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
相关试题

