【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )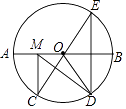
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】∵ ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,
,点E是点D关于AB的对称点,
∴ ![]() =
= ![]() ,
,
∴∠DOB=∠BOE=∠COD= ![]() =60°,∴①正确;
=60°,∴①正确;
∠CED= ![]() ∠COD=
∠COD= ![]() =30°=
=30°= ![]() ,∴②正确;
,∴②正确;
∵ ![]() 的度数是60°,
的度数是60°,
∴ ![]() 的度数是120°,
的度数是120°,
∴只有当M和A重合时,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合时,DM⊥CE,∴③错误;
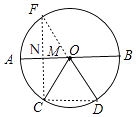
做C关于AB的对称点F,连接CF,交AB于N,连接DF交AB于M,此时CM+DM的值最短,等于DF长,
连接CD,
∵ ![]() =
= ![]() =
= ![]() =
= ![]() ,并且弧的度数都是60°,
,并且弧的度数都是60°,
∴∠D= ![]() =60°,∠CFD=
=60°,∠CFD= ![]() =30°,
=30°,
∴∠FCD=180°﹣60°﹣30°=90°,
∴DF是⊙O的直径,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正确;
故答案为:C.
由已知条件求出,求出∠DOB=∠COD=∠BOE=60°,求出∠CED,即可判断①②;根据圆周角定理求出当M和A重合时∠MDE=60°即可判断③;求出M点的位置,根据圆周角定理得出此时DF是直径,即可求出DF长,即可判断④,最后得到所求的结论..
-
科目: 来源: 题型:
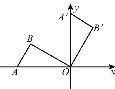
查看答案和解析>>【题目】如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )
A.
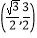 B.
B. 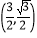
C.
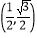 D.
D. 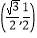
-
科目: 来源: 题型:
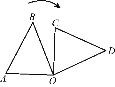
查看答案和解析>>【题目】如图,△AOB绕点O按顺时针方向旋转得到△COD,当OA⊥OC时,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?多少度?
(2)指出线段AB的对应线段,∠A,∠B的对应角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:

(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
-
科目: 来源: 题型:
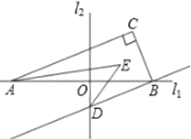
查看答案和解析>>【题目】如图,直线
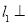 直线
直线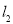 ,垂足为
,垂足为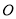 ,
,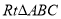 如图放置,过点
如图放置,过点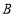 作
作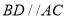 交直线
交直线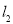 于点
于点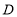 ,在
,在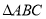 内取一点
内取一点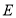 ,连接
,连接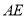 ,
,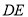 .
.
(1)若
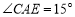 ,
,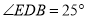 ,则
,则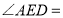 _______.
_______.(2)若
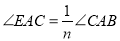 ,
,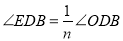 ,则
,则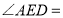 _______°.(用含
_______°.(用含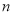 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
相关试题

