搜索
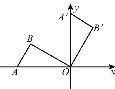
【题目】如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )
A. 
B. 
C. 
D. 
参考答案：
【答案】A
【解析】
利用含30度的直角三角形和勾股定理求出BC和OC，再用旋转的性质得出OC',B'C'，即可解决问题．
解：
在Rt△AOB中，∠AOB=30°，AB=1，
∴OA=2（30°角所对的直角边是斜边的一半）
根据勾股定理得，OB=
=
，
过点B作BC⊥OA于C，
在Rt△BOC中，BC=
OB=
，根据勾股定理得，OC=
=
，
过点B'作B'C'⊥OA'于C'，
由旋转知，B'C'=BC=，OC'=OC=，，
∴B′点的坐标为（，）．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=ax+a（a为常数，a≠0）与反比例函数y=
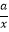（a为常数，a≠0）在同一平面直角坐标系内的图象大致为（ ）
A.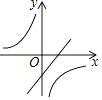
B.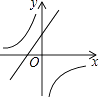
C.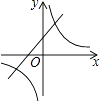
D.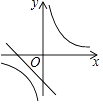
-
科目： 来源： 题型：
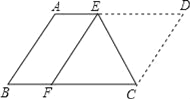
查看答案和解析>>【题目】如图，将ABCD沿CE折叠，使点D落在BC边上的F处，点E在AD上．
（1）求证：四边形ABFE为平行四边形；
（2）若AB=4，BC=6，求四边形ABFE的周长．
-
科目： 来源： 题型：
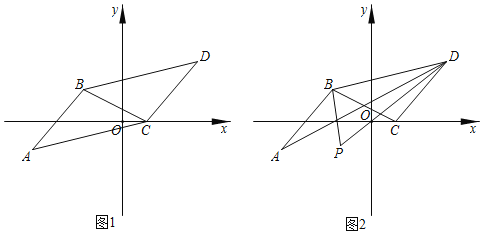
查看答案和解析>>【题目】如图，如图1，在平面直角坐标系中，已知点A（﹣4，﹣1）、B（﹣2，1），将线段AB平移至线段CD，使点A的对应点C在x轴的正半轴上，点D在第一象限．
（1）若点C的坐标（k，0），求点D的坐标（用含k的式子表示）；
（2）连接BD、BC，若三角形BCD的面积为5，求k的值；
（3）如图2，分别作∠ABC和∠ADC的平分线，它们交于点P，请写出∠A、和∠P和∠BCD之间的一个等量关系，并说明理由．
-
科目： 来源： 题型：
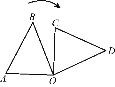
查看答案和解析>>【题目】如图,△AOB绕点O按顺时针方向旋转得到△COD,当OA⊥OC时,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?多少度?
(2)指出线段AB的对应线段,∠A,∠B的对应角.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊙O中，AB是⊙O的直径，AB=10，
= 
= 
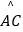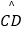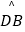，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE=60°；②∠CED= 
∠DOB；③DM⊥CE；④CM+DM的最小值是10，上述结论中正确的个数是（ ）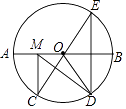
A.1
B.2
C.3
D.4
相关试题
