【题目】如图,已知AB是⊙O的直径,BC为弦,过圆心O作OD⊥BC交弧BC于点D,连接DC,若∠DCB=32°,则∠BAC= . 
参考答案:
【答案】64°
【解析】解:∵∠BOD与∠BCD为 ![]() 所对的圆心角和圆周角, ∴∠BOD=2∠BCD=64°,
所对的圆心角和圆周角, ∴∠BOD=2∠BCD=64°,
∵AB为直径,∴AC⊥BC,
又∵OD⊥BC,∴AC∥OD,
∴∠BAC=∠BOD=64°,
所以答案是:64°.
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( )
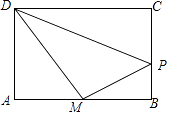
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
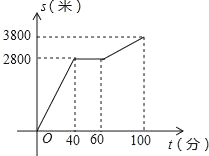
A. 小明中途休息用了20分钟
B. 小明休息前爬山的平均速度大于休息后爬山的平均速度
C. 小明在上述过程中所走的路程为6600米
D. 小明休息前爬山的平均速度为每分钟70米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE : EC=4 : 1,则线段DE的长为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是 .
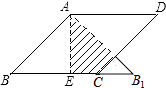
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
 的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D. 
(1)求这两个函数的解析式:
(2)求△ADC的面积.
相关试题

