【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() 的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D. 
(1)求这两个函数的解析式:
(2)求△ADC的面积.
参考答案:
【答案】
(1)解:∵反比例函数y= ![]() 的图象过B(4,﹣2)点,
的图象过B(4,﹣2)点,
∴k=4×(﹣2)=﹣8,
∴反比例函数的解析式为y=﹣ ![]() ;
;
∵反比例函数y= ![]() 的图象过点A(﹣2,m),
的图象过点A(﹣2,m),
∴m=﹣ ![]() =4,即A(﹣2,4).
=4,即A(﹣2,4).
∵一次函数y=ax+b的图象过A(﹣2,4),B(4,﹣2)两点,
∴ ![]() ,
,
解得 ![]()
∴一次函数的解析式为y=﹣x+2;
(2)解:
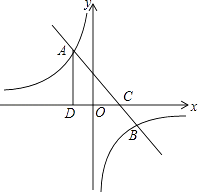
∵直线AB:y=﹣x+2交x轴于点C,
∴C(2,0).
∵AD⊥x轴于D,A(﹣2,4),
∴CD=2﹣(﹣2)=4,AD=4,
∴S△ADC= ![]() CDAD=
CDAD= ![]() ×4×4=8.
×4×4=8.
【解析】(1)因为反比例函数过A、B两点,所以可求其解析式和m的值,从而知A点坐标,进而求一次函数解析式;(2)先求出直线AB与与x轴的交点C的坐标,再根据三角形的面积公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,BC为弦,过圆心O作OD⊥BC交弧BC于点D,连接DC,若∠DCB=32°,则∠BAC= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE : EC=4 : 1,则线段DE的长为______.

-
科目: 来源: 题型:
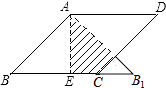
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是 .
-
科目: 来源: 题型:
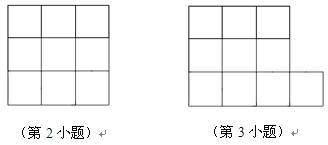
查看答案和解析>>【题目】如图,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开后拼成一个大正方形。

(1)拼成的大正方形的面积与边长分别是多少?
(2)你能在下图3×3方格中,连接四个格点,组成面积为5的正方形吗?
(3)你还能把十个小正方形组成的图形纸,剪开并拼成更大的正方形吗?若能,请在下图中画出图形,并求出它的边长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点B(a,5)在第二象限,点C在y轴上移动,以BC为斜边作等腰直角△BCD,我们发现直角顶点D点随着C点的移动也在一条直线上移动,这条直线的函数表达式是 .
相关试题

