【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
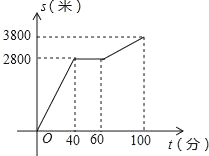
A. 小明中途休息用了20分钟
B. 小明休息前爬山的平均速度大于休息后爬山的平均速度
C. 小明在上述过程中所走的路程为6600米
D. 小明休息前爬山的平均速度为每分钟70米
参考答案:
【答案】C
【解析】
根据函数图象可知,小明40分钟爬山2800米,40~60分钟休息,60~100分钟爬山(3800﹣2800)米,爬山的总路程为3800米,根据路程、速度、时间之间的关系进行解答即可.
选项A,由图象可知,小明中途休息用了60﹣40=20分钟,正确;
选项B,小明休息前爬山的速度为![]() (米/分钟),小明休息后爬山的速度是
(米/分钟),小明休息后爬山的速度是![]() =25(米/分钟),小明休息前爬山的平均速度大于休息后爬山的平均速度,正确;
=25(米/分钟),小明休息前爬山的平均速度大于休息后爬山的平均速度,正确;
选项C,小明在上述过程中所走的路程为3800米,错误;
选项D,小明休息前爬山的速度为![]() (米/分钟),正确;
(米/分钟),正确;
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: ①所调查的七年级50名学生在这个月内做好事次数的平均数是 , 众数是 , 极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
【答案】解:①平均数;(2×5+3×6+4×13+5×16+6×10)÷50=4.4;
众数:5次;
极差:6﹣2=4;
②做好事不少于4次的人数:800× =624;
=624;
(1)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球. ①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?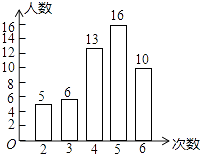
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( )
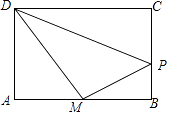
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,BC为弦,过圆心O作OD⊥BC交弧BC于点D,连接DC,若∠DCB=32°,则∠BAC= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE : EC=4 : 1,则线段DE的长为______.

-
科目: 来源: 题型:
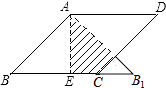
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是 .
相关试题

