搜索
【题目】下列各组条件中，能判断两个直角三角形全等的是（ ）
A. 两组直角边对应相等
B. 一组边对应相等
C. 两组锐角对应相等
D. 一组锐角对应相等
参考答案：
【答案】A
【解析】试题分析：利用SAS、HL、AAS进行判定．
解：A、可以利用边角边判定两三角形全等，故本选项正确；
B、两直角三角形隐含一个条件是两直角相等，要判定两直角三角形全等，起码还要两个条件，则选项错误；
C、两个锐角分别相等，只有角没有边，不能判定全等，此选项错误；
D、一组锐角对应相等，隐含一个条件是两直角相等，根据角对应相等，不能判定三角形全等，故选项错误．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，已知直线y=﹣
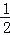x+3分别交x轴，y轴于点A，点B．点P是射线AO上的一个动点．把线段PO绕点P逆时针旋转90°得到的对应线段为PO′，再延长PO′到C使CO′=PO′，连结AC，设点P坐标为（m，0），△APC的面积为S．（1）直接写出OA和OB的长，OA的长是 ，OB的长是 ；
（2）当点P在线段OA上（不含端点）时，求S关于m的函数表达式；
（3）当以A，P，C为顶点的三角形和△AOB相似时，求出所有满足条件的m的值；
（4）如图②，当点P关于OC的对称点P′落在直线AB上时，m的值是 ．
-
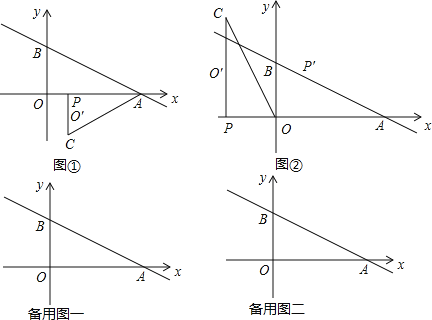
科目： 来源： 题型：
查看答案和解析>>【题目】已知：直线AB与直线CD相交于点O，∠BOC=45°，
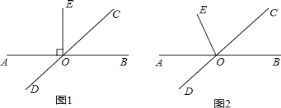
（1）如图1，若EO⊥AB，求∠DOE的度数；
（2）如图2，若EO平分∠AOC，求∠DOE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学习有理数得乘法后，老师给同学们这样一道题目：计算：49
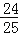×（﹣5），看谁算的又快又对，有两位同学的解法如下：小明：原式=﹣
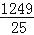×5=﹣
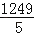=﹣249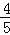
；小军：原式=（49+
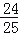）×（﹣5）=49×（﹣5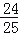）+×（﹣5）=﹣249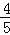；（1）对于以上两种解法，你认为谁的解法较好？
（2）上面的解法对你有何启发，你认为还有更好的方法吗？如果有，请把它写出来；
（3）用你认为最合适的方法计算：19
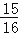×（﹣8） -
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题：①负数没有立方根，②一个实数的立方根不是正数就是负数，③一个正数或负数的立方根与这个数的符号一致，④如果一个数的立方根等于它本身，那么它一定是1或0.其中正确的是( )
A、1 B、2 C、3 D、4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图、矩形ABCD中，AB=8，AD=6．点M是对角线AC上的一个动点，以M点为圆心，线段AM长为半径画一个⊙M，若⊙M在以C为端点的矩形ABCD边上截得的线段EF=
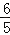AM，则线段AM的长是 ．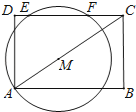
-
科目： 来源： 题型：
查看答案和解析>>【题目】[背景知识]数轴是初中数学的一个重要工具，利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上A点、B点表示的数为a、b，则A，B两点之间的距离AB=|a﹣b|，若a＞b，则可简化为AB=a﹣b；线段AB的中点M表示的数为
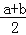．[问题情境]
已知数轴上有A、B两点，分别表示的数为﹣10，8，点A以每秒3个单位的速度沿数轴向右匀速运动，点B以每秒2个单位向左匀速运动．设运动时间为t秒（t＞0）．
[综合运用]
（1）运动开始前，A、B两点的距离为 ；线段AB的中点M所表示的数 ．
（2）点A运动t秒后所在位置的点表示的数为 ；点B运动t秒后所在位置的点表示的数为 ；（用含t的代数式表示）
（3）它们按上述方式运动，A、B两点经过多少秒会相遇，相遇点所表示的数是什么？
（4）若A，B按上述方式继续运动下去，线段AB的中点M能否与原点重合？若能，求出运动时间，并直接写出中点M的运动方向和运动速度；若不能，请说明理由．（当A，B两点重合，则中点M也与A，B两点重合）
相关试题
