【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为![]() .
.
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
参考答案:
【答案】(1)18,-1;(2)﹣10+3t,8﹣2t;(3)A、B两点经过![]() 秒会相遇,相遇点所表示的数是
秒会相遇,相遇点所表示的数是![]() ;(4)经过2秒A,B两点的中点M会与原点重合.M点的运动方向向右,运动速度为每秒
;(4)经过2秒A,B两点的中点M会与原点重合.M点的运动方向向右,运动速度为每秒![]() 个单位长度.理由见解析
个单位长度.理由见解析
【解析】试题分析:(1)根据A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b及线段AB的中点M表示的数为![]() 即可求解;
即可求解;
(2)点A运动t秒后所在位置的点表示的数=运动开始前A点表示的数+点A运动的路程,点B运动t秒后所在位置的点表示的数=运动开始前B点表示的数﹣点B运动的路程;
(3)设它们按上述方式运动,A、B两点经过x秒会相遇,等量关系为:点A运动的路程+点B运动的路程=18,依此列出方程,解方程即可;
(4)设A,B按上述方式继续运动t秒线段AB的中点M能否与原点重合,根据线段AB的中点表示的数为0列出方程,解方程即可.
解:(1)运动开始前,A、B两点的距离为8﹣(﹣10)=18;线段AB的中点M所表示的数为![]() =﹣1;
=﹣1;
(2)点A运动t秒后所在位置的点表示的数为﹣10+3t;点B运动t秒后所在位置的点表示的数为8﹣2t;
(3)设它们按上述方式运动,A、B两点经过x秒会相遇,根据题意得﹣10+3x=8﹣2x,
解得x=![]() ,
,
﹣10+3x=![]() .
.
答:A、B两点经过![]() 秒会相遇,相遇点所表示的数是
秒会相遇,相遇点所表示的数是![]() ;
;
(4)由题意得,![]() =0,
=0,
解得t=2,
答:经过2秒A,B两点的中点M会与原点重合.M点的运动方向向右,运动速度为每秒![]() 个单位长度.
个单位长度.
故答案为18,﹣1;﹣10+3t,8﹣2t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组条件中,能判断两个直角三角形全等的是( )
A. 两组直角边对应相等
B. 一组边对应相等
C. 两组锐角对应相等
D. 一组锐角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①负数没有立方根,②一个实数的立方根不是正数就是负数,③一个正数或负数的立方根与这个数的符号一致,④如果一个数的立方根等于它本身,那么它一定是1或0.其中正确的是( )
A、1 B、2 C、3 D、4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图、矩形ABCD中,AB=8,AD=6.点M是对角线AC上的一个动点,以M点为圆心,线段AM长为半径画一个⊙M,若⊙M在以C为端点的矩形ABCD边上截得的线段EF=
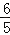 AM,则线段AM的长是 .
AM,则线段AM的长是 .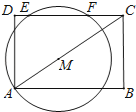
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在
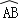 上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )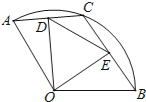
A.先变小,后变大
B.先变大,后变小
C.DE与OD的长度保持相等
D.固定不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,D为BC边上一点,CD=3,过A,C,D三点的⊙O与斜边AB交于点E,连结DE.
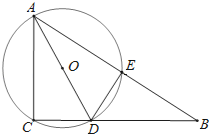
(1)求证:△BDE∽△BAC;
(2)求△ACD外接圆的直径的长;
(3)若AD平分∠CAB,求出BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3个有理数x、y、z,若
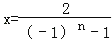 且x与y互为相反数,y与z互为倒数.
且x与y互为相反数,y与z互为倒数.(1)当n为奇数时,你能求出x、y、z这三个数吗?当n为偶数时,你能求出x、y、z这三个数吗?能,请计算并写出结果;不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2011的值.
相关试题

