【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 是双曲线
是双曲线![]() 上不同于
上不同于![]() 的一点,直线
的一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①若![]() ,求
,求![]() 的值;
的值;
②若![]() ,结合图象,直接写出
,结合图象,直接写出![]() 的值.
的值.

参考答案:
【答案】(1)![]() .(2)①
.(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)由直线解析式求得A(2,1),然后代入双曲线y=![]() 中,即可求得k的值;
中,即可求得k的值;
(2)①根据系数k的几何意义即可求得n的值,得到P的坐标,继而求得直线PA的解析式,代入B(b,0)即可求得b的值;②分两种情况讨论求得即可.
(1)∵直线y=![]() x与双曲线y=
x与双曲线y=![]() 的一个交点是A(2,a),
的一个交点是A(2,a),
∴a=![]() ×2=1,
×2=1,
∴A(2,1),
∴k=2×1=2;
(2)①若m=1,则P(1,n),
∵点P(1,n)是双曲线y=![]() 上不同于A的一点,
上不同于A的一点,
∴n=k=2,
∴P(1,2),
∵A(2,1),
则直线PA的解析式为y=-x+3,
∵直线PA与x轴交于点B(b,0),
∴0=-b+3,
∴b=3;
②如图1,当P在第一象限时,
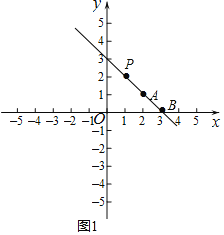
∵PB=2AB,A(2,1),
∴P点的纵坐标时2,
代入y=![]() 求得x=1,
求得x=1,
∴P(1,2),
由①可知,此时b=3;
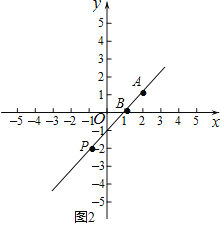
如图2,当P在第,三象限时,
∵PB=2AB,A(2,1),
∴P点的纵坐标时-2,
代入y=![]() 求得x=-1,
求得x=-1,
∴P(-1,-2),
∵A(2,1)
则直线PA的解析式为y=x-1,
∴b=1,
综上,b的值为3或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近视镜镜片的焦距
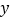 (单位:米)是镜片的度数
(单位:米)是镜片的度数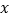 (单位:度)的函数,下表记录了一组数据:
(单位:度)的函数,下表记录了一组数据: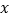 (单位:度)
(单位:度)…
100
250
400
500
…
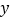 (单位:米)
(单位:米)…
1.00
0.40
0.25
0.20
…
(1)在下列函数中,符合上述表格中所给数据的是_________;
A.
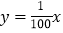 B.
B.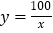 C.
C.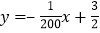 D.
D.
(2)利用(1)中的结论计算:当镜片的度数为200度时,镜片的焦距约为________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.


作法:如图,
①作射线OP;
②在直线OP外任取一点A,以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.
根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴∠BPC=90°(____________)(填推理的依据).
∴OP⊥PC.
又∵OP是⊙O的半径,
∴PC是⊙O的切线(____________)(填推理的依据).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥
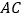 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得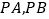 与观光船航向
与观光船航向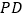 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离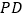 的长.
的长.参考数据:
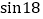 °
°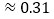 ,
,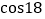 °
°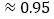 ,
, °
°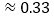 ,
,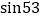 °
°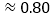 ,
,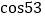 °
°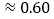 ,
,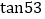 °
°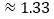 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点C是⊙O中直径AB上的一个动点,过点C作CD⊥AB交⊙O于点D,点M是直径AB上一固定点,作射线DM交⊙O于点N.已知AB=6cm,AM=2cm,设线段AC的长度为xcm,线段MN的长度为ycm.
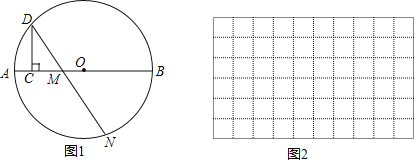
小东根据学习函数的经验,对函数y随自变量的变化而变化的规律进行了探索.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了与y的几组值,如下表:
x/cm
0
1
2
3
4
5
6
y/cm
4
3.3
2.8
2.5
2.1
2
(说明:补全表格时相关数值保留一位小数)
(2)在图2中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AC=MN时,x的取值约为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线G:y=ax2-4ax+3a-2(a≠0),其顶点为C,直线l:y=ax-2a+1(a≠0)与x轴、y轴分别交于A,B两点.
(1)当抛物线G的顶点C在x轴上时,求a的值;
(2)当a>0时,若△ABC的面积为2,求a的值;
(3)若点Q(m,n)在抛物线G上,把抛物线G绕着点P(t,-2)旋转180°,在1≤m≤3时,总有n随着m的增大而增大,请直接写出t的取值范围.

相关试题

