【题目】如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.

参考答案:
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)延长BF、AC交于点M,则结合切线可得BF=FM,再结合平行线分线段成比例可求得CE=DE;
(2)结合条件可证得PF=AF,在Rt△PFB中,可得到PF和PB的关系,再结合PC是切线利用切割线定理可得到PB和PF的关系,可求得PB的长,则可求得AO的长,即⊙O的半径.
(1)证明:如图,延长BF、AC交于点M,
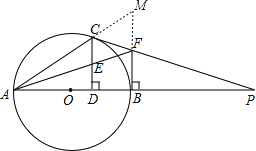
∵BF⊥AB,∴FB是⊙O的切线,
又CF是⊙O的切线,
∴CF=BF,
∴∠FCB=∠FBC,
又AB为直径,
∴∠BCM=90°,
∴∠CBM+∠M=∠BCF+∠FCM=90°,
∴∠FCM=∠M,
∴CF=MF,
∴BF=MF,
∵CD∥MB,
∴![]() ,
,
∴CE=ED,
即E是CD的中点;
(2)解:
∵BF=EF=2=FC=FM,
∴∠FCE=∠FEC=∠AED,
又CD⊥AB,
∴∠FAB+∠AED=∠ECF+∠P,
∴∠FAB=∠P,
∴AF=PF,
∴AB=PB,
设AB=PB=x,PF=y,
则在Rt△PBF中,由勾股定理可得y2=22+x2①,
又由切割线定理可得(y+2)2=x2x=2x2②,
则可解得x=4![]() ,y=6,
,y=6,
∴AO=![]() AB=2
AB=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥
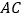 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得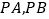 与观光船航向
与观光船航向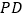 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离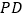 的长.
的长.参考数据:
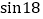 °
°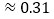 ,
,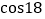 °
°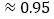 ,
, °
°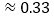 ,
,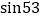 °
°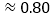 ,
,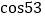 °
°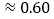 ,
,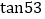 °
°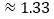 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
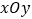 中,已知直线
中,已知直线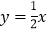 与双曲线
与双曲线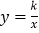 的一个交点是
的一个交点是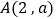 .
.(1)求
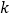 的值;
的值;(2)设点
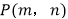 是双曲线
是双曲线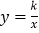 上不同于
上不同于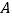 的一点,直线
的一点,直线 与
与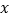 轴交于点
轴交于点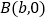 .
.①若
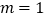 ,求
,求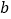 的值;
的值;②若
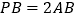 ,结合图象,直接写出
,结合图象,直接写出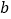 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点C是⊙O中直径AB上的一个动点,过点C作CD⊥AB交⊙O于点D,点M是直径AB上一固定点,作射线DM交⊙O于点N.已知AB=6cm,AM=2cm,设线段AC的长度为xcm,线段MN的长度为ycm.
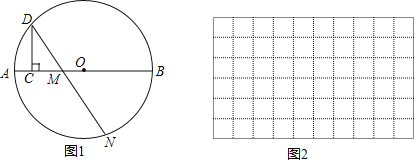
小东根据学习函数的经验,对函数y随自变量的变化而变化的规律进行了探索.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了与y的几组值,如下表:
x/cm
0
1
2
3
4
5
6
y/cm
4
3.3
2.8
2.5
2.1
2
(说明:补全表格时相关数值保留一位小数)
(2)在图2中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AC=MN时,x的取值约为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线G:y=ax2-4ax+3a-2(a≠0),其顶点为C,直线l:y=ax-2a+1(a≠0)与x轴、y轴分别交于A,B两点.
(1)当抛物线G的顶点C在x轴上时,求a的值;
(2)当a>0时,若△ABC的面积为2,求a的值;
(3)若点Q(m,n)在抛物线G上,把抛物线G绕着点P(t,-2)旋转180°,在1≤m≤3时,总有n随着m的增大而增大,请直接写出t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点
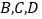 在以点
在以点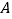 为圆心,
为圆心,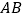 为半径的圆上.
为半径的圆上.②直接写出∠BDC的度数(用含α的式子表示)为___________.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
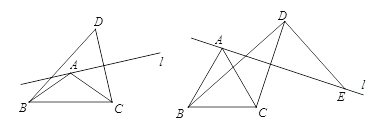
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A在直线l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E.给出如下定义:若线段OE,⊙A和直线l上分别存在点B,点C和点D,使得四边形ABCD是矩形(点A,B,C,D顺时针排列),则称矩形ABCD为直线l的“位置矩形”.
例如,图中的矩形ABCD为直线l的“位置矩形”.

(1)若点A(-1,2),四边形ABCD为直线x=-1的“位置矩形”,则点D的坐标为 ;
(2)若点A(1,2),求直线y=kx+1(k≠0)的“位置矩形”的面积;
(3)若点A(1,-3),直线l的“位置矩形”面积的最大值为 ,此时点D的坐标为 .
相关试题

