搜索
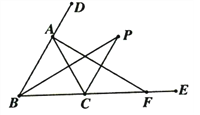
【题目】如图，点F是△ABC的边BC延长线上的一点，且AC=CF，∠ABC和∠ACE的平分线交于点P，下列结论：①点P到△ABC三边的距离相等；②点P在∠DAC的平分线上；③BP垂直平分AC；④CP垂直平分AF；其中正确的判断有______________（只填序号）.
参考答案：
【答案】①②④
【解析】解：∵∠ABC和∠ACE的平分线交于点P，∴P到直线AB的距离=P到直线BC的距离，P到直线AC的距离=P到直线BC的距离，∴P到直线AB的距离=P到直线BC的距离=P到直线AC的距离，故①正确；
∵P到直线AB的距离=P到直线AC的距离，∴点P在∠DAC的平分线上，故②正确；
∵BA不一定等于BC，∴BP垂直平分AC不一定成立，故③错误；
∵AC=CF，CP平分∠ACE，∴CP垂直平分AF，故④正确．
故答案为：①②④．
-
科目： 来源： 题型：
查看答案和解析>>【题目】等腰三角形的两条边长分别是3cm和6cm，则该三角形的周长为（ ）
A. 12cm B. 15cm C. 12cm或15cm D. 9cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，D是BC延长线上的一点，线段BD的垂直平分线EG交AB于点E，交BD于点G．
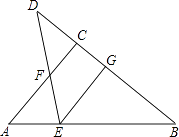
（1）当∠B=30°时，AE和EF有什么关系？请说明理由；
（2）当点D在BC延长线上（CD＜BC）运动时，点E是否在线段AF的垂直平分线上？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某市有甲、乙两种出租车，他们的服务质量相同．甲的计价方式为：当行驶路程不超过3千米时收费10元，每超过1千米则另外收费1.2元（不足1千米按1千米收费）；乙的计价方式为：当行驶路程不超过3千米时收费8元，每超过1千米则另外收费1.8元（不足1千米按1千米收费）．某人到该市出差，需要乘坐的路程为x千米．
（1）当x=5时，请分别求出乘坐甲、乙两种出租车的费用；
（2）用代数式表示此人分别乘坐甲、乙出租车各所需要的费用；
（3）假设此人乘坐的路程为13千米多一点，请问他乘坐哪种车较合算？ -
科目： 来源： 题型：
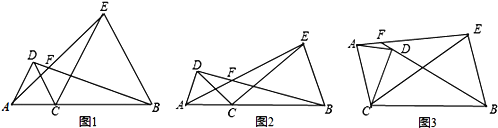
查看答案和解析>>【题目】已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD和△BCE，且CA=CD，CB=CE，∠ACD=∠BCE，直线AE与BD交于点F
（1）如图1，若∠ACD=60゜，则∠AFB= ；
（2）如图2，若∠ACD=α，则∠AFB= （用含α的式子表示）；
（3）将图2中的△ACD绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），如图3．试探究∠AFB与α的数量关系，并予以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答
（1）在数轴上表示下列各数：1.5，0，﹣3，﹣（﹣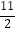
），﹣|﹣4 
|，并用“＜”号把它们连接起来．
（2）根据（1）中的数轴，找出大于﹣|﹣4 |的最小整数和小于﹣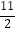（﹣ ）的最大整数，并求出它们的和． -
科目： 来源： 题型：
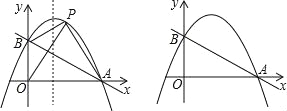
查看答案和解析>>【题目】如图，直线y=﹣
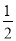x+1与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点．（1）求抛物线的解析式；
（2）点P是第一象限抛物线上的一点，连接PA、PB、PO，若△POA的面积是△POB面积的
倍．①求点P的坐标；
②点Q为抛物线对称轴上一点，请直接写出QP+QA的最小值；
（3）点M为直线AB上的动点，点N为抛物线上的动点，当以点O、B、M、N为顶点的四边形是平行四边形时，请直接写出点M的坐标．
相关试题
