搜索
【题目】解答
（1）在数轴上表示下列各数：1.5，0，﹣3，﹣（﹣ 
），﹣|﹣4 
|，并用“＜”号把它们连接起来．
（2）根据（1）中的数轴，找出大于﹣|﹣4 |的最小整数和小于﹣（﹣ ）的最大整数，并求出它们的和．
参考答案：
【答案】
（1）解：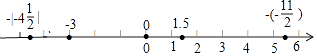 
﹣|﹣4 
|＜﹣3＜0＜1.5＜﹣（﹣ 
）
（2）解：大于﹣|﹣4 |的最小整数是﹣4，小于﹣（﹣ ）的最大整数是5，
和为﹣4+5=1
【解析】（1）先在数轴上表示各个数，再比较即可；（2）先找出最小整数和最大整数，再求出和即可．
【考点精析】本题主要考查了数轴和绝对值的相关知识点，需要掌握数轴是规定了原点、正方向、单位长度的一条直线；正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市有甲、乙两种出租车，他们的服务质量相同．甲的计价方式为：当行驶路程不超过3千米时收费10元，每超过1千米则另外收费1.2元（不足1千米按1千米收费）；乙的计价方式为：当行驶路程不超过3千米时收费8元，每超过1千米则另外收费1.8元（不足1千米按1千米收费）．某人到该市出差，需要乘坐的路程为x千米．
（1）当x=5时，请分别求出乘坐甲、乙两种出租车的费用；
（2）用代数式表示此人分别乘坐甲、乙出租车各所需要的费用；
（3）假设此人乘坐的路程为13千米多一点，请问他乘坐哪种车较合算？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点F是△ABC的边BC延长线上的一点，且AC=CF，∠ABC和∠ACE的平分线交于点P，下列结论：①点P到△ABC三边的距离相等；②点P在∠DAC的平分线上；③BP垂直平分AC；④CP垂直平分AF；其中正确的判断有______________（只填序号）.
-
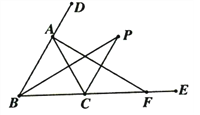
科目： 来源： 题型：
查看答案和解析>>【题目】已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD和△BCE，且CA=CD，CB=CE，∠ACD=∠BCE，直线AE与BD交于点F
（1）如图1，若∠ACD=60゜，则∠AFB= ；
（2）如图2，若∠ACD=α，则∠AFB= （用含α的式子表示）；
（3）将图2中的△ACD绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），如图3．试探究∠AFB与α的数量关系，并予以证明．
-
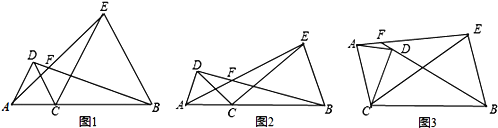
科目： 来源： 题型：
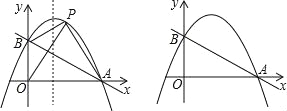
查看答案和解析>>【题目】如图，直线y=﹣
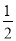x+1与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点．（1）求抛物线的解析式；
（2）点P是第一象限抛物线上的一点，连接PA、PB、PO，若△POA的面积是△POB面积的
倍．①求点P的坐标；
②点Q为抛物线对称轴上一点，请直接写出QP+QA的最小值；
（3）点M为直线AB上的动点，点N为抛物线上的动点，当以点O、B、M、N为顶点的四边形是平行四边形时，请直接写出点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【问题引入】
已知：如图BE、CF是ΔABC的中线，BE、CF相交于G。求证：
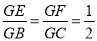
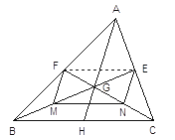
证明：连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF＝
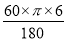BC∴
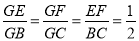
【思考解答】
（1）连结AG并延长AG交BC于H，点H是否为BC中点 （填“是”或“不是”）
（2）①如果M、N分别是GB、GC的中点，则四边形EFMN 是 四边形。
②当
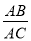的值为 时，四边形EFMN 是矩形。③当
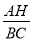的值为 时，四边形EFMN 是菱形。④如果AB＝AC，且AB＝10，BC＝16，则四边形EFMN的面积
＝_________ -
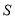科目： 来源： 题型：
查看答案和解析>>【题目】五名男生的体重（单位：kg）分别为50，55，60，55，57，则这组数据的中位数是（ ）
A. 50B. 55C. 57D. 60
相关试题
