【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 边上的动点.将
边上的动点.将![]() 沿AE折叠,点
沿AE折叠,点![]() 落在点
落在点![]() 处;将
处;将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处.当
处.当![]() 的长度为__________时,点
的长度为__________时,点![]() 与点
与点![]() 能重合.
能重合.

参考答案:
【答案】![]()
【解析】
由折叠的性质可得:∠AME=∠B=90°,∠FNE=∠C=90°,∠AEF=![]() ∠BEC=90°,BE=ME,CE=NE,若点
∠BEC=90°,BE=ME,CE=NE,若点![]() 与点
与点![]() 重合,则A、M、F三点共线,进而可得BE=CE
重合,则A、M、F三点共线,进而可得BE=CE![]() ,设DF=CF=x,利用勾股定理分别表示出AE2、EF2、AF2,由此可得关于x的方程,解方程即可求出x,进一步即得结果.
,设DF=CF=x,利用勾股定理分别表示出AE2、EF2、AF2,由此可得关于x的方程,解方程即可求出x,进一步即得结果.
解:由折叠的性质可得:∠AME=∠B=90°,∠FNE=∠C=90°,∠AEM=∠AEB,∠NEF=∠CEF,BE=ME,CE=NE,
若点![]() 与点
与点![]() 重合,则A、M、F三点共线,则BE= ME=NE=CE,∠AEF=
重合,则A、M、F三点共线,则BE= ME=NE=CE,∠AEF=![]() ∠BEC=90°,
∠BEC=90°,
∵![]() ,
,
∴BE=CE=2,
由于点![]() 是
是![]() 边的中点,可设DF=CF=x,则AB=CD=2x,
边的中点,可设DF=CF=x,则AB=CD=2x,
在Rt△AEF中,由勾股定理,得:![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
∴![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
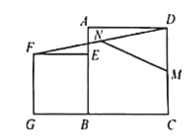
查看答案和解析>>【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且
的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且 ,则四边形
,则四边形 的面积为__________.
的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=
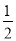 ,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(
,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(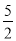 ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( ) 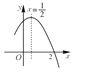
A. ①②④ B. ③④ C. ①③④ D. ①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习新知:如图 1、图 2,
 是矩形
是矩形 所在平面内任意一点,则有以下重要结论:
所在平面内任意一点,则有以下重要结论:  .该结论的证明不难,同学们通过勾股定理即可证明.
.该结论的证明不难,同学们通过勾股定理即可证明.应用新知:如图 3,在
 中,
中, ,
, ,
, 是
是 内一点,且
内一点,且 ,
, ,则
,则 的最小值为__________.
的最小值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD,尺规作图:以点A为圆心,AB的长为半径画弧交AD于点F,分别以点B,F为圆心,以大于 BF的长为半径画弧交于点G,做射线AG交BC与点E,若BF=12,AB=10,则AE的长为( ).

A.17B.16C.15D.14
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OBCD的顶点O在坐标原点,点B的坐标为(2,5),点A在第二象限,反比例函数 的图象经过点A,则k的值是( )
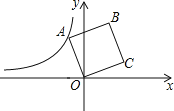
A.
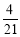 B.
B.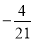 C.
C.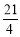 D.
D.
相关试题

