搜索
【题目】如图，已知正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1）．规定“把正方形ABCD先沿x轴翻折，再向左平移一个单位”为一次变换．如此这样，连续经过2018次变换后，正方形ABCD的对角线交点M的坐标为（ ）
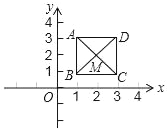
A. （2018，2） B. （2018，﹣2） C. （﹣2016，2） D. （2016，2）
参考答案：
【答案】C
【解析】分析：根据正方形的性质，结合正方形四个顶点的坐标求出对角线点M的坐标；然后根据第1次变换后的点M的对应点的坐标为（2-1，-2），即（1，-2），第2次变换后的点M的对应点的坐标为：（2-2，2），即（0，2），第3次变换后的点M的对应点的坐标为（2-3，-2），即（-1，-2），第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2）；最后利用找到的规律求出经过2018次变换后，正方形对角线交点M的坐标即可.
详解：∵正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1），
∴对角线交点M的坐标为（2，2），
根据题意得：第1次变换后的点M的对应点的坐标为（2-1，-2），即（1，-2），
第2次变换后的点M的对应点的坐标为：（2-2，2），即（0，2），
第3次变换后的点M的对应点的坐标为（2-3，-2），即（-1，-2），
第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2），
∴连续经过2018次变换后，正方形ABCD的对角线交点M的坐标变为（-2016，2）.
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y=
x2﹣
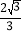x﹣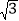
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，点E（4，n）在抛物线上．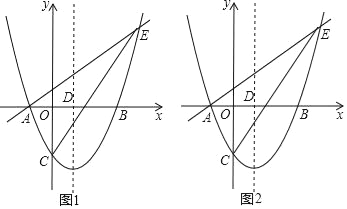
（1）求直线AE的解析式；
（2）点P为直线CE下方抛物线上的一点，连接PC，PE．当△PCE的面积最大时，求P点坐标？
（3）点G是线段CE的中点，将抛物线y=
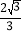x2﹣x﹣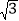沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F．在新抛物线y′的对称轴上，是否存在点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．
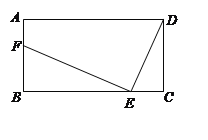
（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若
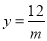，要使△DEF为等腰三角形，m的值应为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】用一些相同的小立方块搭一个几何体，使它从正面看和从上面看的形状图如图所示，从上面看的形状图中小正方形中的字母表示在位置的小立方块的个数，解答下列问题.
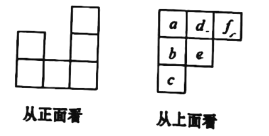
（1）
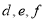各表示几？（2）当
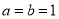时，画出这个几何体从左面看到的形状图. -
科目： 来源： 题型：
查看答案和解析>>【题目】家庭过期药品属于“国家危险废物”，处理不当将污染环境，危害健康．某市药监部门为了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调査．
（1）下列选取样本的方法最合理的一种是 ．（只需填上正确答案的序号）
①在市中心某个居民区以家庭为单位随机抽取；②在全市医务工作者中以家庭为单位随机抽取；③在全市常住人口中以家庭为单位随机抽取．
（2）本次抽样调査发现，接受调査的家庭都有过期药品，现将有关数据呈现如图：
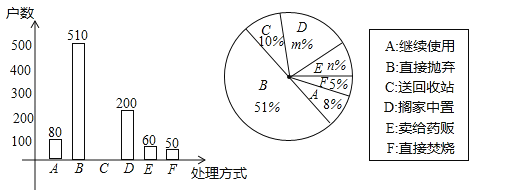
①m= ，n= ；
②补全条形统计图；
③根据调査数据，你认为该市市民家庭处理过期药品最常见的方式是什么？
④家庭过期药品的正确处理方式是送回收点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在ABCD中，点E是BC的中点，连接AE并延长交DC的延长线于点F，连接BF．
(1)求证：△ABE≌△FCE；
(2)若AF＝AD，求证：四边形ABFC是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
(l)概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
(2)性质探宄：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论:（要求用文字语言叙述）
写出证明过程（先画出图形，写出已知、求证）
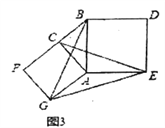
(3)问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5,求GE长．
相关试题
