【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
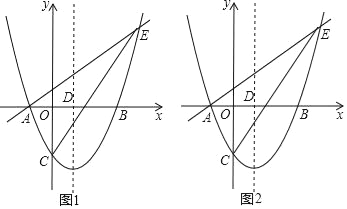
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,求P点坐标?
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) y= ![]() x+
x+ ![]() (2) P(2,﹣
(2) P(2,﹣![]() )(3) (3,
)(3) (3,![]() )或(3,
)或(3,![]() )或(3,2
)或(3,2![]() )或(3,﹣
)或(3,﹣![]() )
)
【解析】试题分析:(1)抛物线的解析式可变形为y=![]() (x+1)(x-3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;
(x+1)(x-3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;
(2)设直线CE的解析式为y=mx-![]() ,将点E的坐标代入即可确定直线CE的解析式,过点P作PF∥y轴,交CE与点F,设点P的坐标为(x,
,将点E的坐标代入即可确定直线CE的解析式,过点P作PF∥y轴,交CE与点F,设点P的坐标为(x,![]() x2
x2![]() x
x![]() ),求出PF的值,表示出△EPC的面积,再利用二次函数的性质可求得x的值,从而得到点P的坐标;
),求出PF的值,表示出△EPC的面积,再利用二次函数的性质可求得x的值,从而得到点P的坐标;
(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为FG=FQ、GF=GQ,QG=QF三种情况求解即可.
解:(1)∵y=![]() x2-
x2-![]() x-
x-![]() ,
,
∴y=![]() (x+1)(x-3).
(x+1)(x-3).
∴A(-1,0),B(3,0).
当x=4时,y=![]() .
.
∴E(4,![]() ),
),
设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:
 ,
,
计算得出:k=![]() ,b=
,b=![]() ,
,
∴直线AE的解析式为y=![]() x+
x+![]()
(2)设直线CE的解析式为y=mx-![]() ,将点E的坐标代入得4m-
,将点E的坐标代入得4m-![]() =
=![]() ,计算出m=
,计算出m=![]() .
.
∴直线CE的解析式为y=![]() x-
x-![]() .
.
过点P作PF∥y轴,交CE与点F,如图①所示.
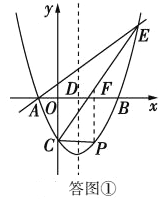
设点P的坐标为(x,![]() x2
x2![]() x
x![]() ),则点F(x,
),则点F(x,![]() x
x![]() ),
),
则FP=(![]() x
x![]() )-(
)-(![]() x2
x2![]() x
x![]() )=-
)=-![]() x2+
x2+![]() x,
x,
∴△EPC的面积=![]() ×(-
×(-![]() x2+
x2+![]() x)×4=-
x)×4=-![]() x2+
x2+![]() x.
x.
∴当x=2时,△EPC的面积最大.
∴P(2,-![]() ).
).
(3)如图②所示:
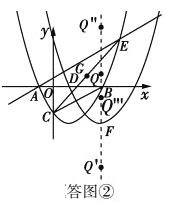
∵y′经过点D,y′的顶点为点F,
∴点F(3,-![]() ).
).
∵点G为CE的中点,
∴G(2,![]() ).
).
∴FG=![]() ,.
,.
∴当FG=FQ时,点Q(3,![]() ),Q′(3,
),Q′(3,![]() ).
).
当GF=GQ时,点F与点Q″关于y=![]() 对称,
对称,
∴点Q″(3,2![]() ).
).
当QG=QF时,设点Q1的的坐标为(3,a).
由两点间的距离公式可以知道:a+![]() =
=![]() ,计算得出:a=-
,计算得出:a=-![]() .
.
∴点Q1的坐标为(3,-![]() ).
).
综上所述,点Q的坐标为(3,![]() )或(3,
)或(3,![]() )或(3,2
)或(3,2![]() )或(3,-
)或(3,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,函数
中,函数 的图象与直线
的图象与直线 交于点A(3,m).
交于点A(3,m).(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于
 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.
的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
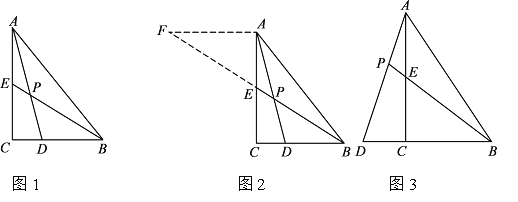
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求
 的值.
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:
 的值为 .
的值为 .参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求
 的值;
的值;(2)若CD=2,则BP=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年8月第29届奥运会将在北京开幕,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2008年8月8日20时应是( )
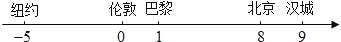
A. 伦敦时间2008年8月8日11时
B. 巴黎时间2008年8月8日13时
C. 纽约时间2008年8月8日5时
D. 汉城时间2008年8月8日19时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
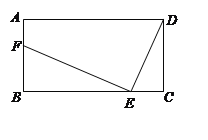
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若
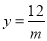 ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】用一些相同的小立方块搭一个几何体,使它从正面看和从上面看的形状图如图所示,从上面看的形状图中小正方形中的字母表示在位置的小立方块的个数,解答下列问题.
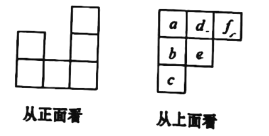
(1)
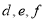 各表示几?
各表示几?(2)当
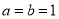 时,画出这个几何体从左面看到的形状图.
时,画出这个几何体从左面看到的形状图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移一个单位”为一次变换.如此这样,连续经过2018次变换后,正方形ABCD的对角线交点M的坐标为( )
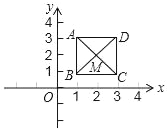
A. (2018,2) B. (2018,﹣2) C. (﹣2016,2) D. (2016,2)
相关试题

