【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
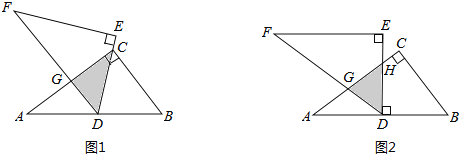
参考答案:
【答案】(1)、6;(2)、![]() .
.
【解析】
试题分析:(1)、根据题意得出△ABC和△FDE全等,从而得出CG和DG的大小,然后根据三角形的面积计算法则求出三角形的面积;(2)、根据题意得出△ABC和△FDE全等,根据Rt△ABC的勾股定理求出AB的长度,根据中点得出AD的长度。连接BH,根据Rt△ADH的勾股定理求出DH的长度,从而得出△DGH的面积.
试题解析:(1)、∵∠ACB=90°,D是AB的中点,∴DC=DB=DA.∴∠B=∠DCB.又∵△ABC≌△FDE,
∴∠FDE=∠B.∴∠FDE=∠DCB.∴DG∥BC.∴∠AGD=∠ACB=90°.∴DG⊥AC.又∵DC=DA,
∴G是AC的中点.∴![]() .∴
.∴![]()
(2)、如图2所示:∵△ABC≌△FDE,∴∠B=∠1.∵∠C=90°,ED⊥AB,∴∠A+∠B=90°,∠A+∠2=90°,
∴∠B=∠2,∴∠1=∠2,∴GH=GD,∵∠A+∠2=90°,∠1+∠3=90°,∴∠A=∠3,∴AG=GD,
∴AG=GH,∴点G为AH的中点; 在Rt△ABC中,![]() ,
,
∵D是AB中点,∴![]() ,
,
连接BH.∵DH垂直平分AB,∴AB=BH.设AH=x,则BH=x,CH=8-x,
由勾股定理得:(8-x)2+62=x2,解得x=, ∴DH=![]() .
.
∴S△DGH=S△ADH=×××5=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
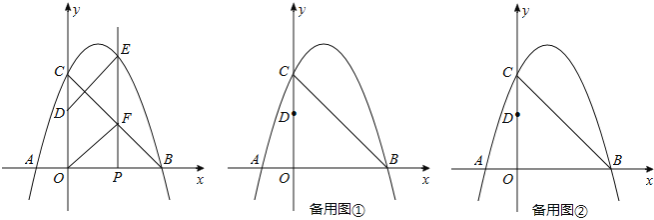
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能判断四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC -
科目: 来源: 题型:
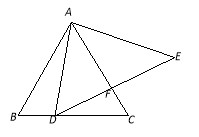
查看答案和解析>>【题目】如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,垂足为F,求∠BAD和∠EDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
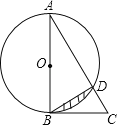
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为 .

相关试题

