【题目】为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
参考答案:
【答案】(1)1号线,2号线每千米的平均造价分别是6亿元和5.5亿元;(2)还需投资660.96亿元.
【解析】
试题分析:(1)假设1号线,2号线每千米的平均造价分别是x亿元,y亿元,根据“修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线的平均造价多0.5亿元”分别得出等式求出即可;
(2)根据(1)中所求得出建91.8千米的地铁线网,每千米的造价,进而求出即可.
解:(1)设1号线,2号线每千米的平均造价分别是x亿元,y亿元,
由题意得出:![]() ,
,
解得:![]() ,
,
答:1号线,2号线每千米的平均造价分别是6亿元和5.5亿元;
(2)由(1)得出:
91.8×6×1.2=660.96(亿元),
答:还需投资660.96亿元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b],对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=
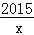 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k>0)是闭区间[m,n]上的“闭函数”,求此函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M关于y轴的对称点的坐标是( )
A.(2,3)
B.(﹣2,3)
C.(﹣3,2)
D.(﹣3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
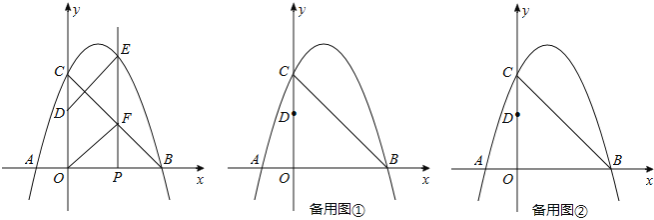
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能判断四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
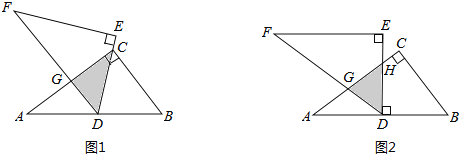
-
科目: 来源: 题型:
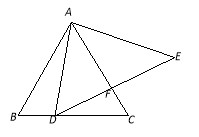
查看答案和解析>>【题目】如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,垂足为F,求∠BAD和∠EDC的度数.
相关试题

