【题目】如图所示,在完全重合放置的两张矩形纸片ABCD中,AB=4,BC=8,将上面的矩形纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分的面积为 .

参考答案:
【答案】![]() .
.
【解析】
试题分析:由于AF=CF,则在Rt△ABF中由勾股定理求得AF的值,证得△ABF≌△AGE,有AE=AF,即ED=AD﹣AE,再由直角三角形的面积公式求得Rt△AGE中边AE上的高的值,即可计算阴影部分的面积.
解:由题意知,AF=FC,AB=CD=AG=4,BC=AD=8
在Rt△ABF中,由勾股定理知AB2+BF2=AF2,即42+(8﹣AF)2=AF2,
解得:AF=5,
∵∠BAF+∠FAE=∠FAE+∠EAG=90°,
∴∠BAF=∠EAG,
∵∠B=∠AGE=90°,AB=AG,
∴△BAF≌△GAE,
∴AE=AF=5,ED=GE=3
∵S△GAE=![]() AGGE=
AGGE=![]() AEAE边上的高
AEAE边上的高
∴AE边上的高=![]() ,
,
∴S△GED=![]() EDAE边上的高=
EDAE边上的高=![]() ×3×
×3×![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
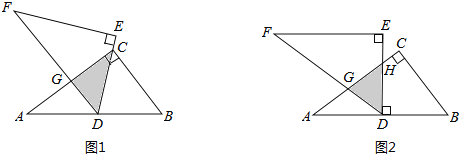
-
科目: 来源: 题型:
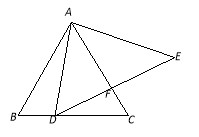
查看答案和解析>>【题目】如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,垂足为F,求∠BAD和∠EDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
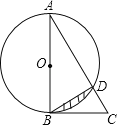
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司的拓展部有五个员工,他们每月的工资分别是3000元,4000元,5000元,7000元和10000元,那么他们工资的中位数是( )
A.4000元 B.5000元 C.7000元 D.10000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一组数据:3,5,5,6,7,这组数据的众数为( )
A.3 B.5 C.6 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校八年级1 000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,在这个问题中,总体是指( )
A.1000名学生
B.被抽取的50名学生
C.1000名学生的身高
D.被抽取的50名学生的身高
相关试题

