【题目】请在横线上填上合适的内容,完成下面的证明:
如图,射线AH交折线ACGFEN于点B、D、E.已知∠A=∠1,∠C=∠F,BM平分∠CBD,EN平分∠FEH.求证:∠2=∠3.

证明:∵∠A=∠1(已知)
∴AC∥GF( )
∴( )( )
∵∠C=∠F(已知)
∴∠F=∠G
∴( )( )
∴( )( )
∵BM平分∠CBD,EN平分∠FEH
∴∠2= ∠3=
∴∠2=∠3
参考答案:
【答案】见解析.
【解析】
依据平行线的判定以及性质,即可得到∠C=∠G,即可得到∠F=∠G,进而判定CG∥EF,再根据平行线的性质,即可得到∠CBD=∠FEH,依据角平分线的定义,即可得出结论.
∵∠A=∠1(已知),
∴AC∥GF(内错角相等,两直线平行),
∴∠C=∠G(两直线平行,内错角相等),
∵∠C=∠F(已知),
∴∠F=∠G,
∴CG∥EF(内错角相等,两直线平行),
∴∠CBD=∠FEH(两直线平行,同位角相等),
∵BM平分∠CBD,EN平分∠FEH,
∴∠2=![]() ∠CBD,∠3=
∠CBD,∠3=![]() ∠FEH,
∠FEH,
∴∠2=∠3,
故答案为:内错角相等,两直线平行,∠C=∠G,两直线平行,内错角相等,CG∥EF,内错角相等,两直线平行,∠CBD=∠FEH,两直线平行,同位角相等,![]() ∠CBD,
∠CBD,![]() ∠FEH.
∠FEH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
 中,
中, 。点
。点 从
从 出发,沿
出发,沿 路线运动,到
路线运动,到 停止;点
停止;点 出发时的速度为每秒
出发时的速度为每秒 ,7秒时点
,7秒时点 的速度变为每秒
的速度变为每秒 ,图②是点
,图②是点 出发
出发 秒后,
秒后, 的面积
的面积 与
与 (秒)的关系图象;
(秒)的关系图象;
(1)根据题目提供的信息,求出
 的值为______________、
的值为______________、 的值为_________
的值为_________ 的值为___________;
的值为___________;(2)设点
 离开点
离开点 的路程为
的路程为 ,
,①7.5秒时,
 的值为_____________________;
的值为_____________________;②请求出当动点
 改变速度后,
改变速度后, 与
与 的关系式;
的关系式;(3)点
 出发后几秒,
出发后几秒, 的面积
的面积 是长方形
是长方形 面积的
面积的 ?并说明理由。
?并说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,对于任意两点
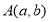 ,
,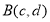 ,若点
,若点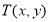 满足
满足 ,
,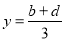 ,那么称点
,那么称点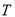 是点
是点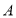 ,
,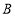 的融合点.
的融合点.例如:
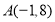 ,
,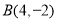 ,当点
,当点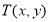 满是
满是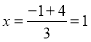 ,
, 时,则点
时,则点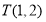 是点
是点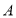 ,
,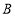 的融合点,
的融合点,
(1)已知点
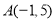 ,
,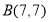 ,
,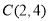 ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.(2)如图,点
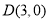 ,点
,点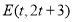 是直线
是直线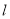 上任意一点,点
上任意一点,点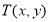 是点
是点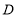 ,
,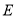 的融合点.
的融合点.①试确定
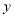 与
与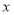 的关系式.
的关系式.②若直线
 交
交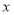 轴于点
轴于点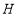 ,当
,当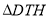 为直角三角形时,求点
为直角三角形时,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,
 ,
,  ,△CDE中,
,△CDE中,  ,CD=DE=5,
,CD=DE=5,连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若
 三点共线,
三点共线,  为
为 中点.
中点.①直接指出
 与
与 的关系______________;
的关系______________;②直接指出
 的长度______________;
的长度______________;(2)将图(1)中的△CDE绕
 点逆时针旋转
点逆时针旋转 (如图2,
(如图2,  ),试确定
),试确定 与
与 的关系,并说明理由;
的关系,并说明理由;(3)在(2)中,若
 ,请直接指出点
,请直接指出点 所经历的路径长.
所经历的路径长.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 交
交 轴于点
轴于点 、点
、点 ,交
,交 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.(1)求
 两点的坐标;
两点的坐标;(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点
 异于
异于 ,且
,且 在对称轴右侧),直线
在对称轴右侧),直线 交对称轴于N,
交对称轴于N,直线BE交对称轴于
 ,对称轴交
,对称轴交 轴于
轴于 ,试确定
,试确定 、
、 的数量关系并说明理由.
的数量关系并说明理由.
-
科目: 来源: 题型:
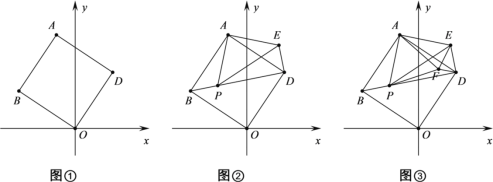
查看答案和解析>>【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.

相关试题

