【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
参考答案:
【答案】(1)![]() ,且
,且![]() ;(2)不存在,理由见试题解析.
;(2)不存在,理由见试题解析.
【解析】
试题(1)根据方程有两个不相等的实数根可知△=![]() ,求得k的取值范围;
,求得k的取值范围;
(2)可假设存在实数k,使得方程的两个实数根![]() ,
,![]() 的倒数和为0,列出方程即可求得k的值,然后把求得的k值代入原式中看看与已知是否矛盾,如果矛盾则不存在,如果不矛盾则存在.
的倒数和为0,列出方程即可求得k的值,然后把求得的k值代入原式中看看与已知是否矛盾,如果矛盾则不存在,如果不矛盾则存在.
试题解析:(1)∵方程有两个不相等的实数根,
∴△=![]() ,且
,且![]() ,解得
,解得![]() ,且
,且![]() ,即k的取值范围是
,即k的取值范围是![]() ,且
,且![]() ;
;
(2)假设存在实数k,使得方程的两个实数根![]() ,
,![]() 的倒数和为0,则
的倒数和为0,则![]() ,
,![]() 不为0,且
不为0,且![]() ,即
,即![]() ,且
,且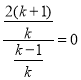 ,解得
,解得![]() ,而
,而![]() 与方程有两个不相等实根的条件
与方程有两个不相等实根的条件![]() ,且
,且![]() 矛盾,故使方程的两个实数根的倒数和为0的实数k不存在.
矛盾,故使方程的两个实数根的倒数和为0的实数k不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
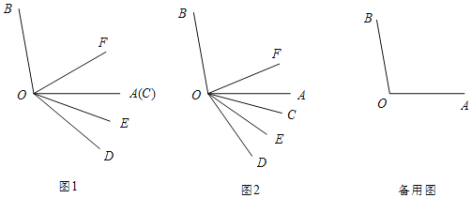
查看答案和解析>>【题目】已知∠AOB=100°,∠COD=40°,OE,OF分别平分∠AOD,∠BOD.
(1)如图1,当OA,OC重合时,求∠EOF的度数;
(2)若将∠COD的从图1的位置绕点O顺时针旋转,旋转角∠AOC=α,且0°<α<90°.
①如图2,试判断∠BOF与∠COE之间满足的数量关系并说明理由.
②在∠COD旋转过程中,请直接写出∠BOE,∠COF,∠AOC之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠BDC=30°,DC=4,AE⊥BD于E,CF⊥BD于F,且E、F恰好是BD的三等分点,AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.
 B.
B. C.2
C.2 D.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有(提示:直角三角形斜边上的中线等于斜边的一半)( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,反向延长线段AB到C,使BC=
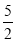 AB,D为BC的中点,E为BD的中点.
AB,D为BC的中点,E为BD的中点.(1)①补全图形;
②若AB=4,则AE=_____(直接写出结果).
(2)若AE=2,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售
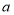 元,在果园每千克售
元,在果园每千克售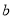 元
元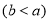 .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用
 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.(2)若
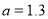 元,
元,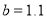 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
相关试题

