【题目】某公园的门票价格如下表所示:

某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如 果两个班联合起来,作为一个团体购票,则需付 1078 元.
(1)列方程求出两个班各有多少学生;
(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮 他们买票呢?请给出最省钱的方案.
参考答案:
【答案】(1)七(1)班有47人,七(2)班有51人;(2) 如果两个班联合起来买票,不可以买单价为9 元的票, 省钱的方法,可以买101张票,多余的作废即可
【解析】
(1)由两个班联合起来,作为一个团体购票,则需付 1078 元可知:![]() 可得票价不是9元,所以两个班的总人数没有超过100人,设七(1)班有x人,七(2)班有y人,可列方程组,解方程组即可得答案;(2)如果两班联合起来作为一个团体购票,则每张票11元,省钱的方法,可以买101张票,多余的作废即可。
可得票价不是9元,所以两个班的总人数没有超过100人,设七(1)班有x人,七(2)班有y人,可列方程组,解方程组即可得答案;(2)如果两班联合起来作为一个团体购票,则每张票11元,省钱的方法,可以买101张票,多余的作废即可。
解:(1)∵两个班联合起来,作为一个团体购票,则需付 1078 元
有∵![]() 可得票价不是9元,所以两个班的总人数没有超过100人,
可得票价不是9元,所以两个班的总人数没有超过100人,
∴设七(1)班有x人,七(2)班有y人,依题意得:

∴七(1)班有47人,七(2)班有51人
(2)因为47+51=98<100
∴如果两个班联合起来买票,不可以买单价为9 元的票
∴省钱的方法,可以买101张票,多余的作废即可。可省:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台
(1)至少购进乙种电冰箱多少台?
(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于3的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,△ABC, ∠ABC、∠ACB 的三等分线交于点 E、D, 若∠1=130°,∠2=110°,求∠A 的度数。
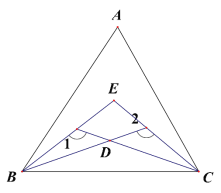
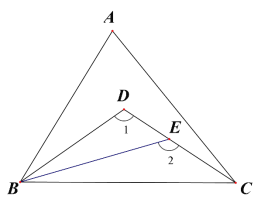
(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E 若∠1=110°,∠2=130°,求∠A 的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 CD 是经过∠BCA 顶点 C 的一条直线,CA=CB.E、F 分别是直线 CD 上两点(不 重合),且∠BEC=∠CFA=∠a
(1)若直线 CD 经过∠BCA 的内部,且 E、F 在射线 CD 上,请解决下面问题:
①若∠BCA=90°,∠a=90°,请在图 1 中补全图形,并证明:BE=CF,EF=
 ;
;②如图 2,若 0°<∠BCA<180°,请添加一个关于∠a 与∠BCA 关系的条件 , 使①中的两个结论仍然成立;
(2)如图 3,若直线 CD 经过∠BCA 的外部,∠a=∠BCA,请写出 EF、BE、AF 三条线 段数量关系(不要求证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三个视图如图所示(单位:cm).

(1)写出这个几何体的名称: ;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家水果店以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是多少斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,且保证每天至少售出260斤,那么水果店需将每斤的售价降低多少元?
相关试题

