【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
(1)如图1,当EF与斜边BC不相交时,试说明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF,BE,CF之间的数量关系,并说明理由;
(3)如图3,猜想EF,BE,CF之间又存在怎样的数量关系,写出猜想,说明理由.

参考答案:
【答案】(1)理由见解析;(2)EF=BE-CF.理由见解析.
【解析】试题分析:(1)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,从而得出答案;(2)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,根据EF=AF-AE得出答案;(3)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,根据EF=AE-AF得出答案.
试题解析:(1)因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFE=90°.
所以∠EAB+∠CAF=90°,∠EBA+∠EAB=90°.所以∠CAF=∠EBA.
在△ABE和△CAF中,∠BEA=∠AFC,∠EBA=∠FAC,AB=AC,所以△BEA≌△AFC(AAS).
所以EA=FC,BE=AF.所以EF=EA+AF=BE+CF.
(2)EF=BE-CF.理由是:因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFE=90°.
所以∠EAB+∠CAF=90°,∠ABE+∠EAB=90°.所以∠CAF=∠ABE.
在△ABE和△ACF中,∠EBA=∠FAC,∠BEA=∠CFA,AB=AC,所以△BEA≌△AFC(AAS).
所以EA=FC,BE=AF.因为EF=AF-AE,所以EF=BE-CF.
(3)EF=CF-BE.理由是:因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFA=90°.
所以∠EAB+∠CAF=90°,∠ABE+∠EAB=90°.
所以∠CAF=∠ABE.在△ABE和△ACF中,∠EBA=∠FAC,∠BEA=∠CFA,AB=AC,
所以△BEA≌△AFC(AAS).
所以EA=FC,BE=CF.因为EF=EA-AF,所以EF=CF-BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线①y=2x2;②y=2(x+1)2﹣5;③y=3(x+1)2;④y=(x+1)2﹣5.其中, 形状相同的是( )
A. ①② B. ②③④ C. ②④ D. ①④
-
科目: 来源: 题型:
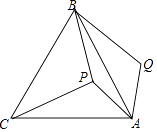
查看答案和解析>>【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=1,b=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生物兴趣小组的同学,将自己收集的标本向本组其他成员各赠送一件,全组共赠送了 210 件,则全组共有_____名同学.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“元旦”期间,小明,小亮等同学随家长一同到我市某景区游玩,下面是买门票时,小明与他爸爸看了票价后的对话:
票价:成人:每张35元; 学生:按成人票价的5折优惠; 团体票(16人以上含16人):按成人票价的a折优惠.
爸爸:大人门票是每张35元,学生门票是5折优惠,我们一共12人,共需350元.
小明:爸爸,等一下,让我算一算,如果按团体票方式买票,还可节省14元.
试根据以上信息,解答以下问题:
(1)小明他们一共去了几个成人?几个学生?
(2)求票价中a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能说明命题“若a>b,则ac>bc”是假命题的一个c值是_____.
相关试题

