【题目】已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC. 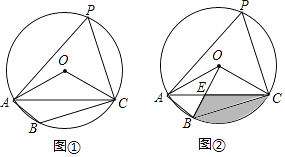
(1)如图①,求∠OCA的度数;
(2)如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ![]() ,求BC的长和阴影部分的面积.
,求BC的长和阴影部分的面积.
参考答案:
【答案】
(1)解:∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°
(2)解:∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC﹣∠AOB=90°,
在Rt△OCE中,OC=2 ![]() ,
,
∴OE=OCtan∠OCE=2 ![]() tan30°=2
tan30°=2 ![]() ×
× ![]() =2,
=2,
∴S△OEC= ![]() OEOC=
OEOC= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() ,
,
∴S扇形OBC= ![]() =3π,
=3π,
∴S阴影=S扇形OBC﹣S△OEC=3π﹣2 ![]()
【解析】(1)根据四边形ABCD是⊙O的内接四边形得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,最后根据OA=OC得到∠OAC=∠OCA=30°;(2)由∠COB为直角,然后利用S阴影=S扇形OBC﹣S△OEC求解.
【考点精析】掌握圆内接四边形的性质和扇形面积计算公式是解答本题的根本,需要知道把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
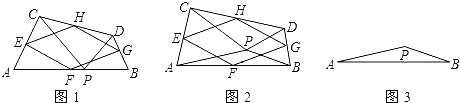
查看答案和解析>>【题目】如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 .
-
科目: 来源: 题型:
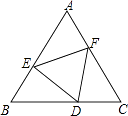
查看答案和解析>>【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P.
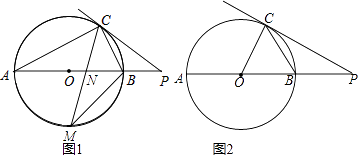
(1)如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;
(2)如图②,若点M是AB的中点,CM交AB于点N,MNMC=36,求BM的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是按规律排列的一列数:
第1个式子:1-
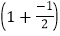 ;
;第2个式子:2-
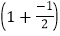 ×
×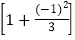 ×
×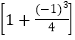 ;
;第3个式子:3-
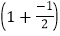 ×
×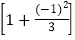 ×
×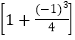 ×
×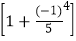 ×
×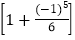 .
.(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2018个式子的形式(中间部分用省略号,两端部分必须写详细),然后计算出结果.
-
科目: 来源: 题型:
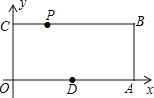
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。

相关试题

