【题目】如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 . 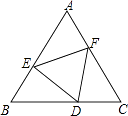
参考答案:
【答案】![]() (a﹣b)
(a﹣b)
【解析】解:如图,由于△ABC,△DEF都为正三角形, ∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
在△AEF和△CFD中,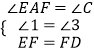 ,
,
∴△AEF≌△CFD(AAS);
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,MH⊥AE于H,
则AH= ![]() (AE+AF﹣EF)=
(AE+AF﹣EF)= ![]() (a﹣b);
(a﹣b);
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AHtan30°= ![]() (a﹣b)
(a﹣b) ![]() =
= ![]() (a﹣b).
(a﹣b).
所以答案是: ![]() (a﹣b).
(a﹣b).
【考点精析】本题主要考查了等边三角形的性质和三角形的内切圆与内心的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)45+(-22)+(-8)-(-5);(2)(-4
 )-(-5
)-(-5 )+(-4
)+(-4 )-3
)-3 ;
;(3)
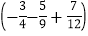 ÷
÷ ; (4)-14+|3-5|-16÷(-2)×
; (4)-14+|3-5|-16÷(-2)× .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为
 ,CD=4,则弦AC的长为( )
,CD=4,则弦AC的长为( ) 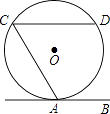
A.2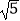
B.3
C.4
D.2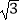
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
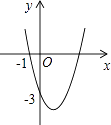
A.﹣3<P<﹣1
B.﹣6<P<0
C.﹣3<P<0
D.﹣6<P<﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 .
-
科目: 来源: 题型:
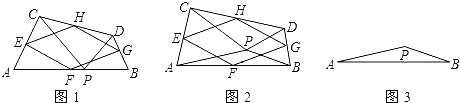
查看答案和解析>>【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC.
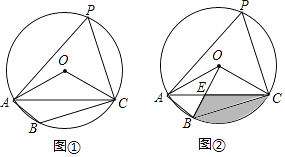
(1)如图①,求∠OCA的度数;
(2)如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ,求BC的长和阴影部分的面积.
,求BC的长和阴影部分的面积.
相关试题

