【题目】已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P. 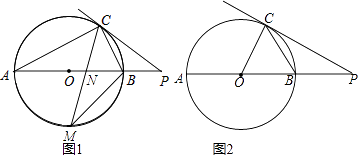
(1)如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;
(2)如图②,若点M是AB的中点,CM交AB于点N,MNMC=36,求BM的值.
参考答案:
【答案】
(1)证明:∵OA=OC,
∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,
∴∠ACO=∠PCB.
∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线
(2)解:连接MA、MB.(如图)
∵点M是弧AB的中点,
∴ ![]() ,
,
∴∠ACM=∠BAM.
∵∠AMC=∠AMN,
∴△AMC∽△NMA.
∴ ![]() .
.
∴AM2=MCMN.
∵MCMN=36,
∴AM=6,
∴BM=AM=6.

【解析】(1)利用半径OA=OC可得∠COB=2∠A,然后利用∠COB=2∠PCB即可证得结论,再根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;(2)连接MA,MB,由圆周角定理可得∠ACM=∠BAM,进而可得△AMC∽△NMA,故AM2=MCMN;等量代换可得MNMC=BM2=AM2 , 代入数据即可得到结论.
【考点精析】通过灵活运用圆周角定理和切线的判定定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 .
-
科目: 来源: 题型:
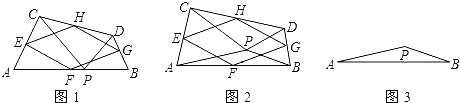
查看答案和解析>>【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC.
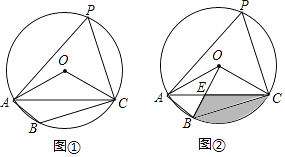
(1)如图①,求∠OCA的度数;
(2)如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ,求BC的长和阴影部分的面积.
,求BC的长和阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是按规律排列的一列数:
第1个式子:1-
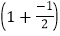 ;
;第2个式子:2-
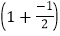 ×
×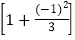 ×
×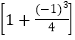 ;
;第3个式子:3-
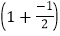 ×
×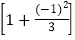 ×
×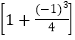 ×
×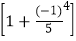 ×
×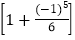 .
.(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2018个式子的形式(中间部分用省略号,两端部分必须写详细),然后计算出结果.
-
科目: 来源: 题型:
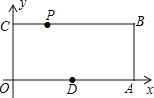
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。

-
科目: 来源: 题型:
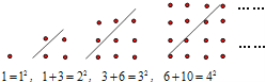
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.用等式表示第100个正方形点阵中的规律_________________.
相关试题

