Question

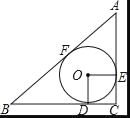
【题目】如图，△ABC中，∠C=90°，⊙O是△ABC的内切圆，D、E、F是切点．

（1）求证：四边形ODCE是正方形；

（2）如果AC=6，BC=8，求内切圆⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）⊙O的半径为2．

【解析】

（1）根据三角形内切圆的性质可得OE⊥AC，OD⊥BC，OE=OD，据此可证明四边形ODCE是正方形；

（2）先根据勾股定理求出AB的长；接下来利用由切线长定理得，AF=AE，BD=BF，CD=CE，由CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB即可求出⊙O的半径为2.

（1）∵⊙O是△ABC的内切圆，

∴OD⊥BC，OE⊥AC，又∠C=90°，

∴四边形ODCE是矩形，

∵OD=OE，

∴四边形ODCE是正方形；

（2）∵∠C=90°，AC=6，BC=8，

∴AB==10，

由切线长定理得，AF=AE，BD=BF，CD=CE，

∴CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB=4，

则CE=2，即⊙O的半径为2．