【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为 . 
参考答案:
【答案】5
【解析】解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF= ![]() AC,
AC,
∴四边形BGFD是菱形,
设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2 , 即(13﹣x)2+62=(2x)2 ,
解得:x=5,
即GF=5.
故答案是:5.
【考点精析】解答此题的关键在于理解直角三角形斜边上的中线的相关知识,掌握直角三角形斜边上的中线等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PE⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2 .
其中结论正确的序号是( )
A.只有①②③
B.只有①③④
C.只有②④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置,得到图2,则下列说法:①阴影部分的周长为4;②当k=1时,图中阴影部分为正六边形;③若阴影部分和空白部分的面积相等,则k=
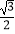 . 其中正确的说法是( )
. 其中正确的说法是( )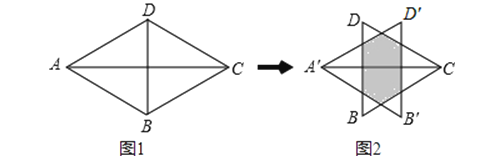
A.①
B.①②
C.②③
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E在BC上,BE=2,CE=1.点P在BD上,则PE与PC的和的最小值为 .
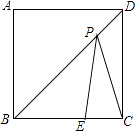
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A.a2a3=a6
B.(a2)3=a5
C.a6÷a2=a3
D.(a2b)2=a4b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如表:
数量(千克)
0.5
1
1.5
2
2.5
3
3.5
…
售价(元)
1.5
3
4.5
6
7.5
9
10.5
…
上表反映了个变量之间的关系,其中,自变量是;因变量是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M , 交y轴于点N , 再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P . 若点P的坐标为(2a , b+1),则a与b的数量关系为( )
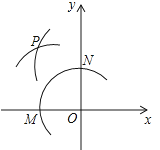
A.a-b
B.2a+b=-1
C.2a-b=l
D.2a+b=l
相关试题

