Question

【题目】如图，已知抛物线y= x2+mx+n（n≠0）与直线y=x交于A、B两点，与y轴交于点C，OA=OB，BC∥x轴．

（1）求抛物线的解析式；
（2）设D、E是线段AB上异于A、B的两个动点（点E在点D的上方），DE= ，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．

Answer 1

【答案】
（1）解：∵抛物线 与y轴交于点C ∴C(0，n)

∵BC∥x轴 ∴B点的纵坐标为n

∵B、A在y=x上，且OA=OB∴B(n，n)，A(-n，-n)

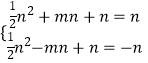∴ 解得：n=0(舍去)，n=-2；m=1

∴所求解析式为：

（2）解：作DH⊥EG于H

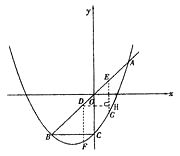
∵D、E在直线y=x上 ∴∠EDH=45 ∴DH=EH

∵DE= ∴DH=EH=1 ∵D(x，x) ∴E(x+1，x+1)

∴F的纵坐标： ，G的纵坐标：

∴DF= -( )=2- EG=(x+1)- [ ]=2-

∴

∴x的取值范围是-2<x<1 当x=- 时，y最大值=3

【解析】 （1）根据题意求出C点的坐标，根据平行于x轴的直线上的点纵坐标相同得出B点的纵坐标为n ，又因B、A在y=x上，故A,B两点的横坐标与纵坐标分别相同，且OA=OB,从而得出B(n，n)，A(-n，-n)，将A,B两点的坐标分别代入函数解析式得出方程组，解出m,n的值，从而得出解析式；
（2）作DH⊥EG于H，由∵D、E在直线y=x上 故∠EDH=45 根据等腰直角三角形的性质得出DH=EH，根据勾股定理得出DH=EH=1，从而知D(x，x) E(x+1，x+1)，进而根据抛物线上点的坐标特点表示出F的纵坐标，G的纵坐标，DF，EG的长度，根据梯形的面积公式列出y与x的函数关系式。