【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.

参考答案:
【答案】(1)55°;(2)①∠FOE=![]() x;②100°.
x;②100°.
【解析】试题分析:(1)、根据对顶角的性质得出∠BOD的度数,根据直角和角平分线的性质求出∠BOF和∠BOE的度数,从而根据∠EOF=∠BOF+∠BOD得出答案;(2)、根据角平分线的性质得出∠BOE=∠DOE,根据平角的性质得出∠COE=∠AOE,最后根据角平分线的性质得出∠FOE的度数;根据题意得出∠BOE= ![]() -15°,根据∠BOE+∠AOE=180°求出x的值,最后根据∠AOC=2∠BOE得出答案.
-15°,根据∠BOE+∠AOE=180°求出x的值,最后根据∠AOC=2∠BOE得出答案.
试题解析:解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,
∵OE平分∠BOD,∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×70°=35°,
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°,
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x,
∵OF平分∠COE, ∴∠FOE=![]() x;
x;
②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=![]() x﹣15°,
x﹣15°,
∵∠BOE+∠AOE=180°,∴![]() x ﹣15°+x=180°,解得:x=130°,
x ﹣15°+x=180°,解得:x=130°,
∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣x+c=0的一个根是﹣2,则c=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
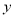 =
=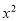 +
+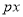 +
+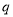 的顶点M是直线
的顶点M是直线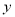 =-
=-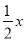 和直线
和直线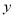 =
= +
+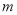 的交点.
的交点.(1)若直线
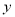 =
=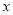 +
+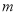 过点D(0,-3),求M点的坐标及二次函数
过点D(0,-3),求M点的坐标及二次函数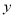 =
=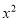 +
+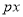 +
+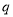 的解析式;
的解析式;(2)试证明无论
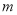 取任何值,二次函数
取任何值,二次函数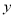 =
=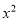 +
+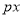 +
+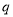 的图象与直线
的图象与直线 =
= +
+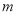 总有两个不同的交点;
总有两个不同的交点;(3)在(1)的条件下,若二次函数
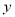 =
=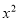 +
+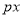 +
+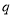 的图象与
的图象与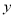 轴交于点C,与
轴交于点C,与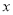 的右交点为A,试在直线
的右交点为A,试在直线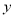 =-
=-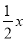 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表述,能确定位置的是( )
A.东经118°,北纬40°
B.江东大桥南
C.北偏东30°
D.某电影院第2排 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程ax2+bx+c=0,若a﹣b+c=0,则该方程一定有一个根是( )
A.﹣1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
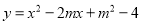 与
与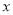 轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.(1)求抛物线的表达式;
(2)若CD∥x轴,点D在点C的左侧,
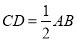 ,求点D的坐标;
,求点D的坐标;(3)在(2)的条件下,将抛物线在直线x=t右侧的部分沿直线x=t翻折后的图形记为G,若图形G与线段CD有公共点,请直接写出t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
相关试题

