【题目】如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD. 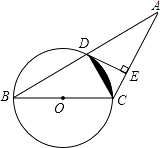
(1)求证:DE为⊙O的切线;
(2)若AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠ODB.又∵∠A=∠B=30°,
∴∠A=∠ODB,
∴DO∥AC,
∵DE⊥AC,
∴OD⊥DE.
∴DE 为⊙O 的切线
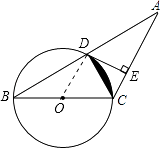
(2)解:∵BC 为直径,
∴∠BDC=90°.
根据等腰三角形的三线合一性质得到CD是AB的中线,
∴BD= ![]() AB=2
AB=2 ![]() ,
,
在直角三角形BDC中,cosB═ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得BC=4,
S阴影=S扇形OCD﹣S△OCD= ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)首先连接OD,根据等边对等角得出∠B=∠ODB,又由等腰三角形ABC的底角为30°,可得∠A=∠ODB,即可证得OD∥AC,继而可证得结论;(2)由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD= ![]() AB=2
AB=2 ![]() ,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD﹣S△OCD即可求得.
,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD﹣S△OCD即可求得.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.
-
科目: 来源: 题型:
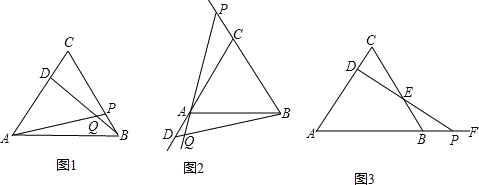
查看答案和解析>>【题目】(9分)探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
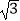 ≈1.7)
≈1.7) 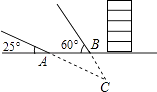
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
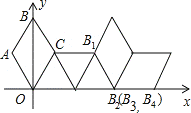
A. (1345,0) B. (1346,0) C. (1345.5,
 ) D. (1346.5,
) D. (1346.5, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体的三视图.
(2)如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数
 (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12 时,OA的长为____.
时,OA的长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点坐标为A(-2.3)、B(-6,0)、C(-1,0)
(1) 将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′ 的坐标________;
(2)将△ABC绕坐标原点O逆时针旋转90°,
直接写出点A的对应点A″的坐标___________;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标___________.

相关试题

