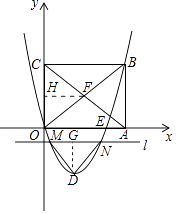
【题目】如图,在平面直角坐标系中,矩形OABC的边OA,OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.
(1)当t=12时,顶点D到x轴的距离等于;
(2)点E是二次函数y=x2+bx(b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(3)矩形OABC的对角线OB、AC交于点F,直线l平行于x轴,交二次函数y=x2+bx(b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
参考答案:
【答案】
(1)![]()
(2)解:将y=0代入抛物线的解析式得:x2+bx=0,解得x=0或x=﹣b,
∵OA=4,
∴AE=4﹣(﹣b)=4+b.
∴OEAE=﹣b(4+b)=﹣b2﹣4b=﹣(b+2)2+4,
∴OEAE的最大值为4,此时b的值为﹣2,
∴抛物线的表达式为y=x2﹣2x.
(3)解:过D作DG⊥MN,垂足为G,过点F作FH⊥CO,垂足为H.
∵△DMN≌△FOC,
∴MN=CO=t,DG=FH=2.
∵D(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴N(﹣ ![]() +
+ ![]() ,﹣
,﹣ ![]() +2),即(
+2),即( ![]() ,
, ![]() ).
).
把点N和坐标代入抛物线的解析式得: ![]() =(
=( ![]() )2+b(
)2+b( ![]() ),
),
解得:t=±2 ![]() .
.
∵t>0,
∴t=2 ![]() .
.
【解析】(1)当t=12时,B(4,12).
将点B的坐标代入抛物线的解析式得:16+4b=12,解得:b=﹣1,
∴抛物线的解析式y=x2﹣x.
∴y=(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
∴D( ![]() ,
, ![]() ).
).
∴顶点D与x轴的距离为 ![]() .
.
所以答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校后勤人员到一家文具店给九年级的同学购买考试用文具包,文具店规定一次购买400个以上,可享受8折优惠.若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,就可享受8折优惠,同样只需付款1936元.请问该学校九年级学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c满足|a-
 |+
|+ +(c-
+(c- )2=0.
)2=0.(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能,求出其周长;若不能,请说明理由.
-
科目: 来源: 题型:
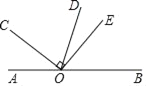
查看答案和解析>>【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°
(1)若∠AOC=40°,求∠BOE和∠DOE的度数;
(2)若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
-
科目: 来源: 题型:
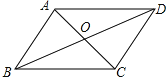
查看答案和解析>>【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.
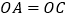 ,
,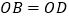 B.
B. 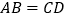 ,
,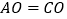
C.
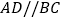 ,
,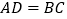 D.
D. 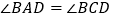 ,
,
相关试题

