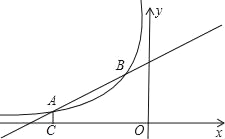
【题目】如图,已知点A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.
(1)求一次函数和反比例函数的解析式;
(2)若P是直线AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P的坐标.
,求点P的坐标.
参考答案:
【答案】(1)y=﹣![]() ;y=
;y=![]() x+
x+![]() ;(2)点P的坐标为(﹣2,
;(2)点P的坐标为(﹣2, ![]() )或(﹣6,﹣
)或(﹣6,﹣![]() ).
).
【解析】试题分析:(1)把点B的坐标代入y=![]() 即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
(2)设点P的横坐标为xP,根据点A的坐标可得到AC的长,然后根据条件即可求出xP,然后将xP代入一次函数的解析式就可求出点P的坐标.
试题解析:
(1)把B(﹣1,2)代入y=![]() ,
,
得m=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣![]() ;
;
把A(﹣4,a)代入y=﹣![]() ,得a=
,得a=![]() ,
,
把A(﹣4, ![]() ),B(﹣1,2)代入y=kx+b,得
),B(﹣1,2)代入y=kx+b,得
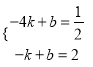 ,
,
解得: 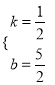 ,
,
∴一次函数解析式为:y=![]() x+
x+![]() ;
;
(2)设点P的横坐标为xP,
∵AC⊥x轴,点A(﹣4, ![]() ),
),
∴AC=![]() .
.
∵△PCA的面积等于![]() ,
,
∴![]() ×
×![]() ×|xP﹣(﹣4)|=
×|xP﹣(﹣4)|=![]() ,
,
解得xP=﹣2或﹣6,
∵P是直线AB上的一点,
∴yP=![]() ×(﹣2)+
×(﹣2)+![]() =
=![]() ,或yP=
,或yP=![]() ×(﹣6)+
×(﹣6)+![]() =﹣
=﹣![]() ,
,
∴点P的坐标为(﹣2, ![]() )或(﹣6,﹣
)或(﹣6,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数
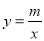 的图象交于点B、E.
的图象交于点B、E.(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
-
科目: 来源: 题型:
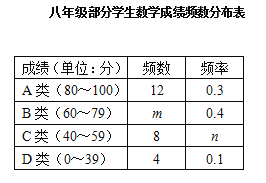
查看答案和解析>>【题目】某中学八年级共有10个班,每班40名学生,学校对该年级学生数学学科某次学情调研测试成绩进行了抽样分析,请按要求回答下列问题:
(1)若要从全年级学生中抽取40人进行调查,你认为以下抽样方法中最合理的是 .
①随机抽取一个班级的40名学生的成绩;
②在八年级学生中随机抽取40名女学生的成绩;
③在八年级10个班中每班各随机抽取4名学生的成绩.
(2)将抽取的40名学生的成绩进行分组,绘制如下成绩频数分布表:
①m= ,n= ;
②根据表格中的数据,请用扇形统计图表示学生成绩分布情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.

(1)本次调查共随机抽取了 名学生;
(2)补全条形统计图;
(3)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为
 ;
;(4)若该区共有10 000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
求证DE=AF.

证法1:∵DE是△ABC的中位线,
∴DE= .
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
-
科目: 来源: 题型:
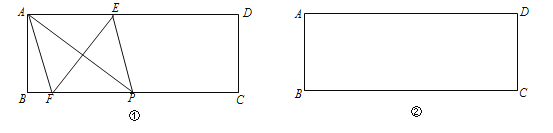
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,BC=3.
(1)在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;
(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
相关试题

