【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,且线段OA、OC(OA>OC)是方程x2﹣18x+80=0的两根,将边BC折叠,使点B落在边OA上的点D处.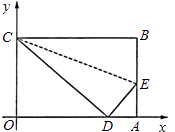
(1)求线段OA、OC的长;
(2)求直线CE与x轴交点P的坐标及折痕CE的长;
(3)是否存在过点D的直线l,使直线CE与x轴所围成的三角形和直线l、直线CE与y轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:方程x2﹣18x+80=0,
因式分解得:(x﹣8)(x﹣10)=0,
即x﹣8=0或x﹣10=0,
解得:x1=8,x2=10,
∴OA=10,OC=8
(2)
解:由折叠可知:△EBC≌△EDC,∴EB=ED,
∴CB=CD,又矩形OABC,∴AB=OC=8,
∴CB=CD=OA=10,又OC=8,
在Rt△OCD中,根据勾股定理得:OD= ![]() =6,
=6,
∴AD=OA﹣OD=10﹣6=4,
又BE+EA=AB=8,且EB=ED,
∴DE+EA=8,即DE=8﹣EA,
在Rt△AED中,设AE=x,则DE=8﹣x,又AD=4,
根据勾股定理得:(8﹣x)2=x2+16,
整理得:16x=48,
解得:x=3,
则E的坐标为(10,3),又C(0,8),
设直线CE的解析式为y=kx+b,
将C与E坐标代入得: ![]() ,
,
解得:k=﹣ ![]() ,b=8,
,b=8,
则直线CE解析式为y=﹣ ![]() x+8,
x+8,
令y=0求出x=16,即P坐标为(16,0);
此时BE=BA﹣EA=8﹣3=5,又BC=OA=10,
在Rt△BCE中,根据勾股定理得:
CE= ![]() =5
=5 ![]()
(3)
解:存在.满足条件的直线l有2条:y=﹣2x+12,y=2x﹣12.
如图2:
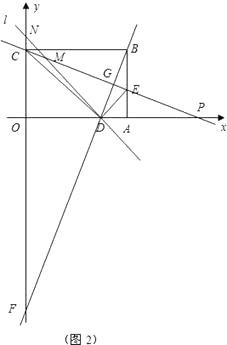
【解析】(1.)利用式子相乘法把方程左边分解为两一次因式积的形式,然后根据两数相乘积为0,两数中至少有一个为0,转化为两个一元一次方程,分别求出方程的解得到原方程的解,根据OA大于OC,即可得到OA及OC的长;(2.)由折叠可知三角形EBC与三角形EDC全等,根据全等三角形的对应边相等得到EB=ED,CB=CD,又矩形ABCD对边相等,从而得到CD的长,再由OC的长,利用勾股定理求出OD的长,进而求出AD的长,在直角三角形AED中,设EA=x,则DE=8﹣x,再由AD的长,利用勾股定理列出关于x的方程,求出方程的解得到AE的长,即为E的纵坐标,而OA的长即为E的横坐标,确定出E的坐标,同时得到BE的长,再由BC的长,在直角三角形BCE中,利用勾股定理求出折痕CE的长;
(3.)存在,应该有两条如图:
①直线BF,根据折叠的性质可知CE必垂直平分BD,那么∠DGP=∠CGF=90°,而∠CFG=∠DPG(都是∠OCP的余角),由此可得出两三角形相似,那么可根据B、D两点的坐标求出此直线的解析式.
②直线DN,由于∠FCO=∠NDO,那么可根据∠OCE即∠BEC的正切值,求出∠NDO的正切值,然后用OD的长求出ON的值,即可求出N点的坐标,然后根据N、D两点的坐标求出直线DN的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年合肥市共有30293名考生参加中考,为了了解这30293名考生的数学成绩,从中抽取了1000名生的数学成绩进行统计分析,以下说法中,错误的是( )
A. 这种调查采用了抽样调查的方式
B. 30293名考生是总体
C. 从中抽取的1000名学生的数学成绩是总体的一个样本
D. 样本容量是1000
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚走路时发现自己的影子越走越长,这是因为( )
A. 从路灯下走开,离路灯越来越远B. 走到路灯下,离路灯越来越近
C. 人与路灯的距离与影子长短无关D. 路灯的灯光越来越亮
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F.
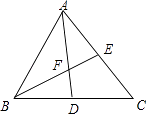
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
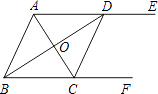
(1)若AB=1,则BC的长=;
(2)求证:四边形ABCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左到右边的变形,是因式分解的是( )
A、(3﹣x)(3+x)=9﹣x2
B、(y+1)(y﹣3)=﹣(3﹣y)(y+1)
C、4yz﹣2y2z+z=2y(2z﹣yz)+z
D、﹣8x2+8x﹣2=﹣2(2x﹣1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】由四舍五入得到的近似数88.35万.精确到( )
A. 十分位 B. 百分位 C. 百位 D. 十位
相关试题

