【题目】如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果![]() ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和![]() 的值.
的值.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)∠CDF的度数为45°,
,证明见解析;(3)∠CDF的度数为45°,![]() 的值为
的值为![]() .
.
【解析】(1)先证明△CDA是等腰三角形,再根据等腰三角形的性质证明AM+CK=MK;在△MKD中,AM+CK>MK(两边之和大于第三边);
(2)作点C关于FD的对称点G,连接GK,GM,GD.证明△ADM≌△GDM后,根据全等三角形的性质,GM=AM,GM+GK>MK,∴AM+CK>MK;
(3)根据勾股定理的逆定理求得∠GKM=90°,又∵点C关于FD的对称点G,∴<CKG=90°,<FKC=![]() <CKG=45°,根据三角形的外角定理,就可以求得∠CDF=15°;在Rt△GKM中,∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°,∴∠GMK=30°,利用余弦定理解得
<CKG=45°,根据三角形的外角定理,就可以求得∠CDF=15°;在Rt△GKM中,∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°,∴∠GMK=30°,利用余弦定理解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,以点
中,以点 为圆心,
为圆心, 长为半径画弧交
长为半径画弧交 于点
于点 ,再分别以点
,再分别以点 、
、 为圆心,大于
为圆心,大于 的相同长为半径画弧,两弧交于点
的相同长为半径画弧,两弧交于点 ,连接
,连接 并延长交
并延长交 于点
于点 ,连接
,连接 ,则所得四边形
,则所得四边形 是菱形.
是菱形.
(1)根据以上尺规作图的过程,求证:四边形
 是菱形.
是菱形.(2)若菱形
 的周长为16,
的周长为16, ,求菱形
,求菱形 的面积及
的面积及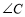 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平分
平分 ,
, 平分
平分 ,
, 与
与 交于
交于 ,若
,若 ,
, ,则
,则 的度数为_________.(用
的度数为_________.(用 表示)
表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是边
是边 上一个动点,过
上一个动点,过 作直线
作直线 分别交
分别交 、外角
、外角 的平分线于点
的平分线于点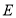 、
、 .
.
(1)若
 ,
, ,求
,求 的长;
的长;(2)连接
 、
、 .问:当点
.问:当点 在边
在边 上运动到什么位置时,四边形
上运动到什么位置时,四边形 是矩形?并说明理由.
是矩形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 经过原点O及点A
经过原点O及点A 和点B
和点B .
.(1)求抛物线的解析式;
(2)如图1,设抛物线的对称轴与x轴交于点C,将直线
 沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;(3)如图2,将抛物线向上平移9个单位得到新抛物线,直接写出下列两个问题的答案:
①直线
 至少向上平移多少个单位才能与新抛物线有交点?
至少向上平移多少个单位才能与新抛物线有交点?②新抛物线上的动点Q到直线
 的最短距离是多少?
的最短距离是多少?
相关试题

