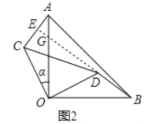
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
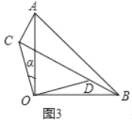
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

参考答案:
【答案】(1)证明见解析;(2)AC=7, ![]()
【解析】试题分析:(1)图形经过旋转以后,明确没有变化的边长,根据全等三角形的判定定理证明图中的△COA≌△DOB,从而证明AC=BD,做辅助△ABE,证明∠AEB=90°,从而得到AC⊥BD;
(2)在△COA中,根据余弦定理,得出cosα的值,从而求出sinα的值.
试题解析:(1)如图2中,延长BD交OA于G,交AC于E.
∵∠AOB=∠COD=90°,
∴∠AOC=∠DOB,
在△AOC和△BOD中, 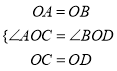 ,
,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
∵∠DBO+∠GOB=90°,
∵∠OGB=∠AGE,
∴∠CAO+∠AGE=90°,
∴∠AEG=90°,
∴BD⊥AC.
(2)如图3中,设AC=x,
∵BD、CD在同一直线上,BD⊥AC,
∴△ABC是直角三角形,
∴AC2+BC2=AB2,
∴x2+(x+17)2=252,
解得x=7,
∵∠ODC=∠α+∠DBO=45°,∠ABC+∠DBO=45°,
∴∠α=∠ABC,
∴sinα=sin∠ABC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
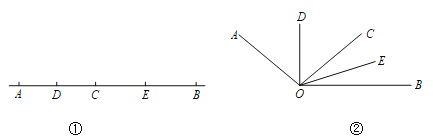
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车的雨刷能把玻璃上的雨水刷干净,这说明( )
A.点动成线
B.线动成面
C.面动成体
D.以上说法都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个角的两边分别平行,其中一个角比另一个角的4倍少30°,这两个角是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和等于它的外角和的5倍,则这个多边形的边数是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
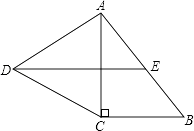
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.所有等边三角形都相似B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似D.所有矩形都相似
相关试题

