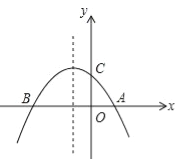
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)点A坐标(2,0),点B坐标(﹣4,0),点C坐标(0,2);(2)![]() ;(3)M坐标为(﹣1,﹣1)或(﹣1,2+
;(3)M坐标为(﹣1,﹣1)或(﹣1,2+![]() )或(﹣1.2﹣
)或(﹣1.2﹣![]() ).
).
【解析】
试题分析:(1)分别令y=0,x=0,解方程后即可得点A,B,C的坐标;(2)分AB为平行四边形的边和对角线两种情况求解决可;(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.
试题解析:(1)令y=0得﹣![]() x2﹣
x2﹣![]() x+2=0,
x+2=0,
∴x2+2x﹣8=0,
x=﹣4或2,
∴点A坐标(2,0),点B坐标(﹣4,0),
令x=0,得y=2,∴点C坐标(0,2).
(2)当AB为平行四边形的边,
∵AB=EF=6,对称轴x=﹣1,
∴点E的横坐标为﹣7或5,
∴点E坐标(﹣7,﹣![]() )或(5,﹣
)或(5,﹣![]() ),此时点F(﹣1,﹣
),此时点F(﹣1,﹣![]() ),
),
∴以A,B,E,F为顶点的平行四边形的面积=6×![]() =
=![]() .
.
当AB为平行四边形的对角线时,点F为抛物线的顶点,即F(-1,![]() ),所以点E的坐标为(-1,-
),所以点E的坐标为(-1,-![]() ),
),
∴以A,B,E,F为顶点的平行四边形的面积=![]() .
.
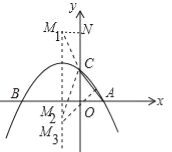
(3)如图所示,①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN=![]() =
=![]() ,
,
∴点M1坐标(﹣1,2+![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣![]() ).
).
②当M3为顶点时,∵直线AC解析式为y=﹣x+1,
线段AC的垂直平分线为y=x,
∴点M3坐标为(﹣1,﹣1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+![]() )或(﹣1.2﹣
)或(﹣1.2﹣![]() ).
).
-
科目: 来源: 题型:
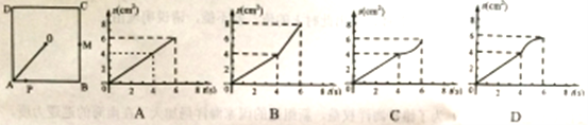
查看答案和解析>>【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1cm/s. 设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图像可以是( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
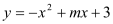 与
与 轴交于A,B两点,与
轴交于A,B两点,与 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴
 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB.
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,试求点O到AB的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(a+1)x+a2﹣1,当a_____时,它是一次函数;当a_____时,它是正比例函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不能作为直角三角形三边长度的是( )
A.2、3、4
B.3、4、5
C.6、8、10
D.25、24、7 -
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,下列事件中的不可能事件是( ).
A.点数之和小于4
B.点数之和为10
C.点数之和为14
D.点数之和大于5且小于9
相关试题

